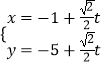题目内容
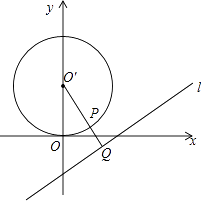
【题目】如图，已知直线l：x+ 
y﹣c=0（c＞0）为公海与领海的分界线，一艘巡逻艇在O处发现了北偏东60°海面上A处有一艘走私船，走私船正向停泊在公海上接应的走私海轮B航行，以使上海轮后逃窜．已知巡逻艇的航速是走私船航速的2倍，且两者都是沿直线航行，但走私船可能向任一方向逃窜． 
（1）如果走私船和巡逻船相距6海里，求走私船能被截获的点的轨迹；
（2）若O与公海的最近距离20海里，要保证在领海内捕获走私船（即不能截获走私船的区域与公海不想交）．则O，A之间的最远距离是多少海里？
【答案】
（1）解：由题意知点A（3 
，3），设走私船能被截获的点为P（x，y），
则|OP|=2|AP|，
即 
=2 
，整理得：（x﹣4 ）2+（y﹣4）2=16．
∴走私船能被截获的点的轨迹是以（4 ，4）为圆心，以4为半径的圆
（2）解：由题意得 
=20，即c=40．∴直线l的方程为x+ y﹣40=0．
设|OA|=t，则A（ 
t， 
t）（t＞0），
设走私船能被截获的点为P（x，y），则|OP|=2|AP|，
∴ =2 
，
整理得：（x﹣ 
t）2+（y﹣ 
t）2= 
，
∴走私船能被截获的点的轨迹是以C（ t， 
）为圆心，以 为半径的圆．
若保证在领海内捕获走私船，则圆心C到直线l的距离d≥ ．
∴ 
≥ t，
解得：t≤ 
=15（ ﹣1），
∴O，A之间的最远距离是15（ ﹣1）海里
【解析】（1）设截获点为P（x，y），根据|OP|=2|AP|列方程化简即可；（2）设|OA|=t，求出截获点轨迹方程，根据直线与圆不相交列不等式得出t的范围即可得出|OA|的最大值．
练习册系列答案
相关题目
