题目内容
【题目】已知双曲线C： 
=1经过点（2，3），两条渐近线的夹角为60°，直线l交双曲线于A，B两点．
（1）求双曲线C的方程；
（2）若l过原点，P为双曲线上异于A，B的一点，且直线PA，PB的斜率kPA ， kPB均存在，求证：kPAkPB为定值；
（3）若l过双曲线的右焦点F1 ， 是否存在x轴上的点M（m，0），使得直线l绕点F1无论怎样转动，都有 
=0成立？若存在，求出M的坐标；若不存在，请说明理由．
【答案】
（1）
解：由题意得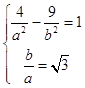 
解得a=1，b= 
∴双曲线C的方程为 
（2）
证明：设A（x0，y0），由双曲线的对称性，可得B（﹣x0，﹣y0）．
设P（x，y），
则kPAkPB= 
，
∵y02=3x02﹣3，y2=3x2﹣3，
所以kPAkPB= =3
（3）
解：由（1）得点F1为（2，0）
当直线l的斜率存在时，设直线方程y=k（x﹣2），A（x1，y1），B（x2，y2）
将方程y=k（x﹣2）与双曲线方程联立消去y得：（k2﹣3）x2﹣4k2x+4k2+3=0，
∴x1+x2= 
，x1x2= 
假设双曲线C上存在定点M，使MA⊥MB恒成立，设为M（m，n）
则 
=（x1﹣m）（x2﹣m）+[k（x1﹣2）﹣n][k（x2﹣2）﹣n]
=（k2+1）x1x2﹣（2k2+kn+m）（x1+x2）+m2+4k2+4kn+n2= 
=0，
故得：（m2+n2﹣4m﹣5）k2﹣12nk﹣3（m2+n2﹣1）=0对任意的k2＞3恒成立，
∴ 
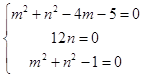，解得m=﹣1，n=0
∴当点M为（﹣1，0）时，MA⊥MB恒成立；
当直线l的斜率不存在时，由A（2，3），B（2，﹣3）知点M（﹣1，0）使得MA⊥MB也成立．
又因为点（﹣1，0）是双曲线C的左顶点，
所以双曲线C上存在定点M（﹣1，0），使MA⊥MB恒成立
【解析】（1）利用双曲线C： 
=1经过点（2，3），两条渐近线的夹角为60°，建立方程，即可求双曲线C的方程；（2）设M（x0 ， y0），由双曲线的对称性，可得N的坐标，设P（x，y），结合题意，又由M、P在双曲线上，可得y02=3x02﹣3，y2=3x2﹣3，将其坐标代入kPMkPN中，计算可得答案．（3）先假设存在定点M，使MA⊥MB恒成立，设出M点坐标，根据数量级为0，求得结论．
