题目内容
17．
某校为了了解高三同学暑假期间学习情况，调查了200名同学，统计他们每天平均学习时间，绘成频率分布直方图（如图）．则这200名同学中学习时间在6～8小时的同学为60人．
分析 根据频率分布直方图，利用频率=$\frac{频数}{样本容量}$，即可求出对应的结果．
解答 解：根据频率分布直方图，得；
这200名同学中学习时间在6～8小时的频率为
1-（0.04+0.12+0.14+0.05）×2=0.3，
所以，这200名同学中学习时间在6～8小时的同学为
200×0.30=60．
故答案为：60．
点评 本题考查了频率分布直方图的应用问题，是基础题目．
练习册系列答案
相关题目
8．在△ABC中，角A，B，C的对边分别为a，b，c，cos2C+2cos（A+B）+$\frac{3}{2}$=0，a+b=5，c=$\sqrt{7}$．
（1）求角C的大小；
（2）求△ABC的面积．
（1）求角C的大小；
（2）求△ABC的面积．
5．已知sinθcosθ＜0，那么角θ是（ ）
| A． | 第一或第二象限角 | B． | 第二或第三象限角 | ||
| C． | 第二或第四象限角 | D． | 第一或第四象限角 |
8．设$\overrightarrow{OM}$=（2，1），$\overrightarrow{ON}$=（0，1），O为坐标原点，动点P（x，y）满足0≤$\overrightarrow{OP}$•$\overrightarrow{OM}$≤1，0≤$\overrightarrow{OP}$•$\overrightarrow{ON}$≤1，则x-y的最小值是（ ）
| A． | $\frac{1}{2}$ | B． | -$\frac{1}{2}$ | C． | $\frac{3}{2}$ | D． | -$\frac{3}{2}$ |
5．如图，在△ABC中，AD⊥AB，$\overrightarrow{BC}$=$\sqrt{3}$$\overrightarrow{BD}$，|$\overrightarrow{AD}$|=1，则$\overrightarrow{AD}$•$\overrightarrow{AC}$的值为（ ）
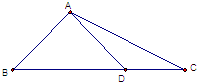
| A． | $\sqrt{3}$ | B． | 3 | C． | $\frac{\sqrt{2}}{2}$ | D． | $\sqrt{5}$ |
的图象如右图所示，则下列函数图象正确的是（ ）
B．
D．