题目内容
2.设等差数列{an}的前n项和Sn=n2-2n (n∈N*),各项均为正数的等比数列{bn}中,b1=a2,b3=a6.(1)求数列{an},{bn}的通项公式;
(2)设数列{cn}满足cn=$\frac{1}{{{a_{n+1}}{a_{n+2}}}}$,Tn为数列{cn}的前n项和.问是否存在正整数m,n(1<m<n),使得T1,Tm,Tn成等比数列?若存在,求出所有m,n的值;若不存在,请说明理由.
分析 (1)利用n=1时,a1=S1,n≥2时,an=Sn-Sn-1,可得an.再利用等比数列的通项公式可得bn.
(2)利用“裂项求和”、等比数列的通项公式、不等式的性质即可得出.
解答 解:(1)n=1时,a1=S1=-1.
n≥2时,an=Sn-Sn-1=2n-3.
上式对n=1也适合,
∴an=2n-3(n∈N*).
则b1=a2=1,b3=a6=9,
∵bn>0,∴b2=3,公比q=3,
∴bn=3n-1.
(2)∵${c_n}=\frac{1}{{{a_{n+1}}{a_{n+2}}}}=\frac{1}{(2n-1)(2n+1)}=\frac{1}{2}(\frac{1}{2n-1}-\frac{1}{2n+1})$,
∴${T_n}=\frac{1}{2}[(1-\frac{1}{3})+(\frac{1}{3}-\frac{1}{5})+…+(\frac{1}{2n-1}-\frac{1}{2n+1})]=\frac{1}{2}(1-\frac{1}{2n+1})=\frac{n}{2n+1}$.
则${T_1}=\frac{1}{3}$,${T_m}=\frac{m}{2m+1}$,${T_n}=\frac{n}{2n+1}$.
设T1,Tm,Tn成等比数列,
则${(\frac{m}{2m+1})^2}=\frac{1}{3}•\frac{n}{2n+1}$.
∴$n=\frac{{3{m^2}}}{{-2{m^2}+4m+1}}$.
令n>0,得2m(m-2)<1.
∵m是正整数,∴m=2.
此时n=12,
因此,当且仅当m=2,n=12时,T1,Tm,Tn成等比数列.
点评 本题考查了等差数列与等比数列的通项公式、“裂项求和”、不等式的性质,考查了推理能力与计算能力,属于中档题.

| A. | 已知购买一张彩票中奖的概率为$\frac{1}{1000}$,则购买1000张这种彩票一定能中奖 | |
| B. | 互斥事件一定是对立事件 | |
| C. | 二进制数1101(2)转化为十进制数是13 | |
| D. | 若样本x1,x2…xn的方差为4,则样本x1-1,x2-1,…,xn-1的方差为3 |
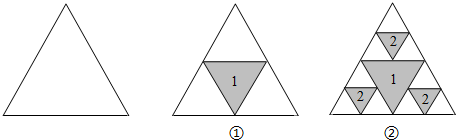
| A. | 0.1 | B. | 0.2 | C. | 0.3 | D. | 0.6 |
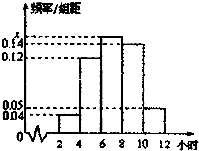 某校为了了解高三同学暑假期间学习情况,调查了200名同学,统计他们每天平均学习时间,绘成频率分布直方图(如图).则这200名同学中学习时间在6~8小时的同学为60人.
某校为了了解高三同学暑假期间学习情况,调查了200名同学,统计他们每天平均学习时间,绘成频率分布直方图(如图).则这200名同学中学习时间在6~8小时的同学为60人.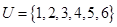 ,集合
,集合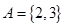 ,集合
,集合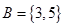 ,则
,则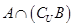 =( )
=( )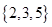 B.
B. C.
C. D.
D.