题目内容
5.如图,在△ABC中,AD⊥AB,→BC−−→BC=√3√3→BD−−→BD,|→AD−−→AD|=1,则→AD−−→AD•→AC−−→AC的值为( )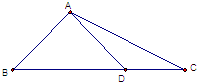
| A. | √3√3 | B. | 3 | C. | √22√22 | D. | √5√5 |
分析 运用向量的数量积的定义,结合条件可得→AD−−→AD•→AC−−→AC=|→AC−−→AC|cos∠DAC,再由诱导公式可得→AD−−→AD•→AC−−→AC=|→AC−−→AC|sin∠BAC,结合三角形ABC中的正弦定理和直角三角形的锐角三角函数的定义,计算即可得到所求值
解答 解:→AD−−→AD•→AC−−→AC=|→AD||→AC|cos∠CAD|−−→AD||−−→AC|cos∠CAD,
∵|→AD−−→AD|=1,
∴→AD−−→AD•→AC−−→AC=|→AC−−→AC|cos∠CAD,
∵∠BAC=π2π2+∠DAC,
∴cos∠CAD=sin∠BAC,
→AD−−→AD•→AC−−→AC=|→AC−−→AC|sin∠BAC,
在△ABC中,由正弦定理得ACsinB=BCsinBACACsinB=BCsinBAC,变形得|AC|sin∠BAC=|BC|sinB,
所以→AD−−→AD•→AC−−→AC=|→AC−−→AC|sin∠BAC=|BC|sinB=|BC|•ADBDADBD=√3√3,
故选A.
点评 本题考查向量的数量积的定义和性质,同时考查诱导公式和正弦定理的运用,属于中档题

练习册系列答案
 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案
相关题目
16.通过随机询问200名性别不同的大学生是否爱好“踢毽子运动”,计算得到统计量值k2的观测值k≈4.892,参照下表,得到的正确结论是( )
| P(k2≥k) | 0.10 | 0.05 | 0.010 |
| k | 2.706 | 3.841 | 6.635 |
| A. | 在犯错误的概率不超过5%的前提下,认为“爱好该运动与性别有关” | |
| B. | 在犯错误的概率不超过5%的前提下,认为“爱好该运动与性别无关” | |
| C. | 有99%以上的把握认为“爱好该运动与性有关” | |
| D. | 有99%以上的把握认为“爱好该运动与性别无关” |
13.下列说法正确的是( )
| A. | 已知购买一张彩票中奖的概率为1100011000,则购买1000张这种彩票一定能中奖 | |
| B. | 互斥事件一定是对立事件 | |
| C. | 二进制数1101(2)转化为十进制数是13 | |
| D. | 若样本x1,x2…xn的方差为4,则样本x1-1,x2-1,…,xn-1的方差为3 |
10.已知随机变量X服从正态分布N(1,σ2),且P(-2≤X≤1)=0.4,则P(X>4)=( )
| A. | 0.1 | B. | 0.2 | C. | 0.3 | D. | 0.6 |
17.已知数若变量x,y满足约束条件{1≤x+y≤23≤4x+y≤4,则z=9x+y的最大值为( )
| A. | -9 | B. | 9 | C. | 6 | D. | -6 |
13.已知△ABC的三条边长分别为3,4,5,如果把三角形的三边都增加相同的长度,则这个新三角形的形状为( )
| A. | 锐角三角形 | B. | 直角三角形 | ||
| C. | 钝角三角形 | D. | 由增加的长度决定 |
 某校为了了解高三同学暑假期间学习情况,调查了200名同学,统计他们每天平均学习时间,绘成频率分布直方图(如图).则这200名同学中学习时间在6~8小时的同学为60人.
某校为了了解高三同学暑假期间学习情况,调查了200名同学,统计他们每天平均学习时间,绘成频率分布直方图(如图).则这200名同学中学习时间在6~8小时的同学为60人. 中,角
中,角 ,
, ,
,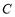 所对的边分别为
所对的边分别为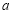 ,
, ,
, ,且满足
,且满足 .
. 的大小;
的大小; ,求
,求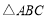 的周长的取值范围.
的周长的取值范围.