题目内容
8.若函数y=f(x),x∈D同时满足下列条件:(1)在D内为单调函数;
(2)?[m,n],使x∈[m,n]时,f(x)的值域为[m,n],则称此函数为D内的可等射函数.
若f(x)=$\frac{{a}^{x}+a-3}{lna}$(a>1)为可等射函数,则a的取值范围为(1,2).
分析 由f(x)为可等射函数,得到ax-xlna+a-3=0有两个不等实根,令g(x)=ax-xlna+a-3,求出其导数后进行分类讨论,能够求出a的取值范围.
解答 解:∵f(x)为可等射函数,
∴f(x)=$\frac{{a}^{x}+a-3}{lna}$=x有两个不等实根,
即ax-xlna+a-3=0有两个不等实根,
令g(x)=ax-xlna+a-3,
∴g′(x)=axlna-lna=lna(ax-1),
令g′(x)=0,得x=0.
当a>1时,x>0时,g′(x)>0,x<0时,g′(x)<0,
∴g(x)min=g(0)=1+a-3<0,
∴a<2,
故1<a<2;
故答案为:(1,2).
点评 本题考查函数的单调性的判断和求实数的取值范围.构造函数,求函数的导数,利用导数研究函数的单调性是解决本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
18.在一个盒子中有大小一样的15个球,其中9个红球,6个白球,甲、乙两人各摸一球,不放回,则在甲摸出红球的条件下,乙摸出白球的概率为( )
| A. | $\frac{4}{7}$ | B. | $\frac{2}{5}$ | C. | $\frac{2}{3}$ | D. | $\frac{3}{7}$ |
18.已知f(x),g(x)分别是定义在R上的偶函数和奇函数,且f(x)-g(x)=x3-2x2,则f(2)+g(2)=( )
| A. | 16 | B. | -16 | C. | 8 | D. | -8 |
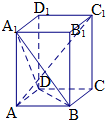 在长方体ABCD-A1B1C1D1中,AB=AD=1,AA1=2,给出下列结论:
在长方体ABCD-A1B1C1D1中,AB=AD=1,AA1=2,给出下列结论: