题目内容
定义在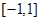 上的奇函数
上的奇函数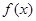 ,当
,当 时,
时,
(1)求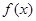 在
在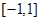 上的解析式;
上的解析式;
(2)判断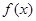 在
在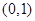 上的单调性,并给予证明;
上的单调性,并给予证明;
(3)当 时,关于
时,关于 的方程
的方程 有解,试求实数
有解,试求实数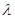 的取值范围.
的取值范围.
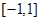 上的奇函数
上的奇函数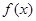 ,当
,当 时,
时,
(1)求
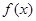 在
在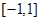 上的解析式;
上的解析式;(2)判断
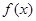 在
在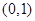 上的单调性,并给予证明;
上的单调性,并给予证明;(3)当
 时,关于
时,关于 的方程
的方程 有解,试求实数
有解,试求实数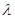 的取值范围.
的取值范围.(1) (2)
(2)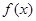 在
在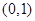 上为减函数,证明见解析(3)
上为减函数,证明见解析(3)
 (2)
(2)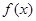 在
在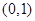 上为减函数,证明见解析(3)
上为减函数,证明见解析(3)
试题分析:(1)∵
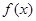 在
在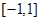 上是奇函数,∴
上是奇函数,∴ , ……1分
, ……1分设
 ,则
,则 ,
, , ……3分
, ……3分 . ……4分
. ……4分(2)设
 ,则
,则 , ……6分
, ……6分∵
 ,∴
,∴ ,
,又
 ,
, ,
,所以
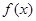 在
在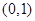 上为减函数. ……8分
上为减函数. ……8分(3)当
 时,
时, ,则方程
,则方程 化为
化为 ……10分
……10分∵
 ,
,
而

 ……11分
……11分因此要使方程
 有解,只须
有解,只须 ……12分
……12分点评:奇函数如果在原点处有定义,则一定有
 ;用定义域证明函数的单调性性时,一定要把结果化到最简,而第三问将问题转化为复合函数的值域问题是解决第三问的关键.
;用定义域证明函数的单调性性时,一定要把结果化到最简,而第三问将问题转化为复合函数的值域问题是解决第三问的关键.
练习册系列答案
相关题目
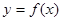 定义在
定义在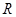 上,对于任意实数
上,对于任意实数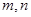 ,恒有
,恒有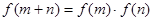 ,且当
,且当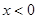 时,
时,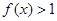
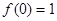 ,且当
,且当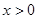 时,
时, 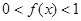
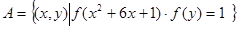 ,
,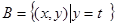 ,且
,且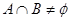 ,
,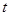 的取值范围.
的取值范围.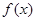 =
=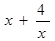
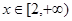 上是增函数;(2)求
上是增函数;(2)求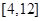 上的值域。
上的值域。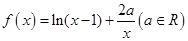 ,
,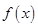 的图像在点
的图像在点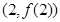 处的切线方程;
处的切线方程;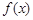 的单调区间;
的单调区间;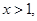 且
且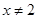 时,
时,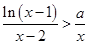 恒成立,求实数
恒成立,求实数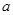 的取值范围。
的取值范围。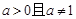 ,函数
,函数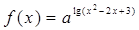 有最大值,则不等式
有最大值,则不等式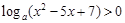 的解集为 .
的解集为 .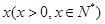 户农民从事蔬菜加工,则剩下的继续从事蔬菜种植的农民平均每户的年收入有望提高
户农民从事蔬菜加工,则剩下的继续从事蔬菜种植的农民平均每户的年收入有望提高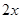 %,而从事蔬菜加工的农民平均每户的年收入将为
%,而从事蔬菜加工的农民平均每户的年收入将为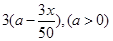 万元.
万元.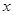 户农民从事蔬菜加工后,要使从事蔬菜种植的农民的总年收入不低于动员前从事蔬菜种植的农民的总年收入,求
户农民从事蔬菜加工后,要使从事蔬菜种植的农民的总年收入不低于动员前从事蔬菜种植的农民的总年收入,求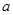 的最大值.
的最大值.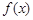 是定义在
是定义在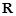 上且周期为2的函数,在区间
上且周期为2的函数,在区间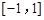 上,
上,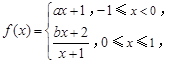 其中
其中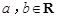 .若
.若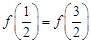 ,则
,则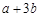 的值为____..
的值为____..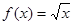 ,则
,则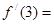 为( )
为( )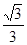
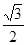
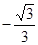
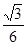
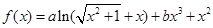 ,其中
,其中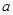 、
、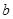 为常数,
为常数,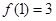 ,则
,则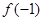 =_________.
=_________.