题目内容
设函数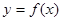 定义在
定义在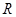 上,对于任意实数
上,对于任意实数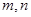 ,恒有
,恒有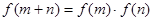 ,且当
,且当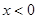 时,
时,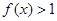
(1)求证: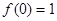 ,且当
,且当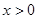 时,
时, 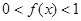
(2)求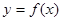 在
在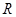 上的单调性.
上的单调性.
(3)设集合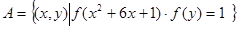 ,
,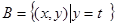 ,且
,且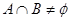 ,
,
求实数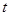 的取值范围.
的取值范围.
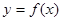 定义在
定义在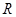 上,对于任意实数
上,对于任意实数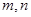 ,恒有
,恒有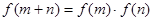 ,且当
,且当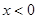 时,
时,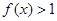
(1)求证:
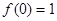 ,且当
,且当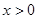 时,
时, 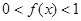
(2)求
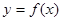 在
在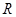 上的单调性.
上的单调性.(3)设集合
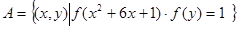 ,
,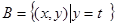 ,且
,且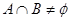 ,
,求实数
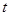 的取值范围.
的取值范围.(1)见解析;(2) 在
在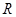 上是减函数. (3)
上是减函数. (3)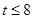 。
。
 在
在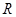 上是减函数. (3)
上是减函数. (3)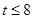 。
。试题分析:(1)证明:取
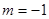 ,
, ,由已知
,由已知
则
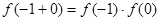 ,
,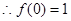 -----------2分
-----------2分 当
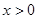 时,
时, 时,则
时,则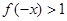
由
 得
得
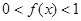 ----------4分
----------4分(2)任取
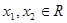 ,且
,且 .
.则
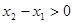
 -----------5分
-----------5分 
 -----------6分
-----------6分 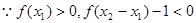
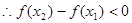 即
即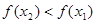
 在
在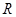 上是减函数. -----------8分
上是减函数. -----------8分解(3)在集合
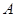 中,
中,

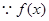 在
在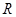 上是减函数
上是减函数  -------10分
-------10分
 ,
,  ---------12分
---------12分 点评:不给出具体解析式,只给出函数的特殊条件或特征的函数即为抽象函数。一般的:①求抽象函数的函数值常用赋值法。②证明抽象函数的单调性常用定义法。

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
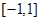 上的奇函数
上的奇函数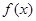 ,当
,当 时,
时,
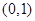 上的单调性,并给予证明;
上的单调性,并给予证明; 时,关于
时,关于 的方程
的方程 有解,试求实数
有解,试求实数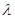 的取值范围.
的取值范围.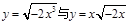
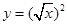 与
与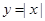

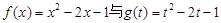
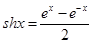 和双曲余弦函数
和双曲余弦函数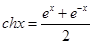 ,双曲正弦函数和双曲余弦函数与我们学过的正弦函数和余弦函数有许多相类似的性质,请类比正、余弦函数的和角或差角公式,写出关于双曲正弦、双曲余弦函数的一个正确的类似公式 。
,双曲正弦函数和双曲余弦函数与我们学过的正弦函数和余弦函数有许多相类似的性质,请类比正、余弦函数的和角或差角公式,写出关于双曲正弦、双曲余弦函数的一个正确的类似公式 。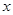 为实数,则
为实数,则 与
与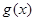 表示同一个函数的是 ( )
表示同一个函数的是 ( ) 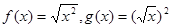

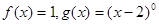

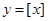 称为高斯函数,又称取整函数,对任意实数
称为高斯函数,又称取整函数,对任意实数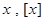 是不超过
是不超过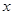 的最大整数,则函数
的最大整数,则函数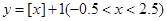 的值域为 .
的值域为 . 
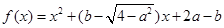 是偶函数,则函数图像与
是偶函数,则函数图像与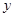 轴交点的纵坐标的最大值是( ).
轴交点的纵坐标的最大值是( ).