题目内容
设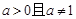 ,函数
,函数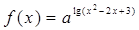 有最大值,则不等式
有最大值,则不等式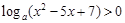 的解集为 .
的解集为 .
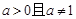 ,函数
,函数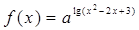 有最大值,则不等式
有最大值,则不等式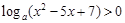 的解集为 .
的解集为 .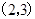
试题分析:因为函数
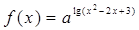 有最大值,而
有最大值,而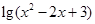 有最小值,所以
有最小值,所以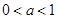 ,所以由不等式
,所以由不等式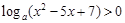 可以得出
可以得出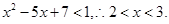
点评:复合函数的单调性满足同增异减,而通过复合函数的单调性判断出
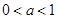 是解决本题的关键.
是解决本题的关键.
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
题目内容
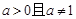 ,函数
,函数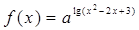 有最大值,则不等式
有最大值,则不等式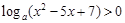 的解集为 .
的解集为 .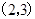
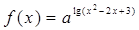 有最大值,而
有最大值,而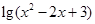 有最小值,所以
有最小值,所以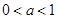 ,所以由不等式
,所以由不等式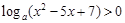 可以得出
可以得出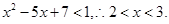
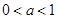 是解决本题的关键.
是解决本题的关键.
 阅读快车系列答案
阅读快车系列答案