题目内容
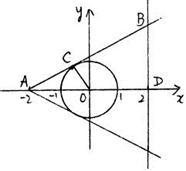
已知圆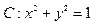 ,点
,点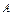 (-2,0)及点
(-2,0)及点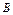 (2,
(2,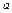 ),从
),从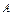 点观察
点观察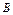 点,要使视线不被圆
点,要使视线不被圆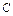 挡住,则
挡住,则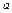 的取值范围是( )
的取值范围是( )
A.(-∞,-1)∪(-1,+∞) B.(-∞,-2)∪(2,+∞)
C.(-∞,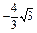 )∪(
)∪(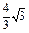 ,+∞) D.(-∞,-4)∪(4,+∞)
,+∞) D.(-∞,-4)∪(4,+∞)
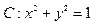 ,点
,点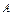 (-2,0)及点
(-2,0)及点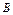 (2,
(2,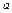 ),从
),从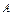 点观察
点观察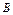 点,要使视线不被圆
点,要使视线不被圆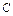 挡住,则
挡住,则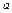 的取值范围是( )
的取值范围是( )A.(-∞,-1)∪(-1,+∞) B.(-∞,-2)∪(2,+∞)
C.(-∞,
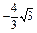 )∪(
)∪(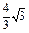 ,+∞) D.(-∞,-4)∪(4,+∞)
,+∞) D.(-∞,-4)∪(4,+∞)C
分析(一)直接法
写出直线方程,利用直线与圆相切
解方程组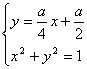 消去y,并整理,得
消去y,并整理,得
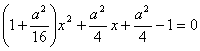
直线与圆相切的主要条件为
△=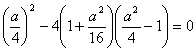
解得a=±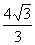
再进一步判断便可得正确答案为(C).
分析(二)直接法:写出直线方程,将直线与圆相切转化为点到直线的距离来解决.
过A、B两点的直线方程为y=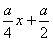 ,即 ax-4y+2a=0
,即 ax-4y+2a=0
则a=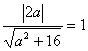 化简后,得3a2=16,解得a=±
化简后,得3a2=16,解得a=±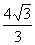 .
.
再进一步判断便可得到正确答案为(C).
分析(三)数形结合法
在Rt△AOC中,由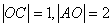 ,可求出∠CAO=30°.
,可求出∠CAO=30°.
在Rt△BAD中,由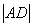 =4,∠BAD=30°,可求得BD=
=4,∠BAD=30°,可求得BD=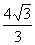 ,再由图直观判断,应选(C).
,再由图直观判断,应选(C).
写出直线方程,利用直线与圆相切
解方程组
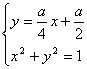 消去y,并整理,得
消去y,并整理,得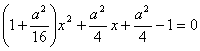
直线与圆相切的主要条件为
△=
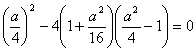
解得a=±
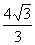
再进一步判断便可得正确答案为(C).
分析(二)直接法:写出直线方程,将直线与圆相切转化为点到直线的距离来解决.
过A、B两点的直线方程为y=
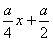 ,即 ax-4y+2a=0
,即 ax-4y+2a=0则a=
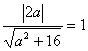 化简后,得3a2=16,解得a=±
化简后,得3a2=16,解得a=±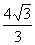 .
.再进一步判断便可得到正确答案为(C).
分析(三)数形结合法
在Rt△AOC中,由
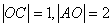 ,可求出∠CAO=30°.
,可求出∠CAO=30°.在Rt△BAD中,由
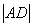 =4,∠BAD=30°,可求得BD=
=4,∠BAD=30°,可求得BD=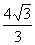 ,再由图直观判断,应选(C).
,再由图直观判断,应选(C).

练习册系列答案
 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目
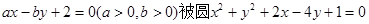 截得的弦长为4,则
截得的弦长为4,则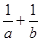 最小值是 ( )
最小值是 ( )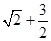


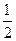 =0与圆(x-cosβ)2+(y+sinβ)2=
=0与圆(x-cosβ)2+(y+sinβ)2=

 ,使得
,使得 是以点E为直角顶点的等腰直角三角形。
是以点E为直角顶点的等腰直角三角形。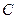
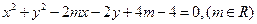
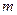 的值,使圆
的值,使圆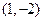 的直线方程.
的直线方程.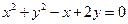 关于直线
关于直线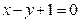 对称的圆的方程 .
对称的圆的方程 .