题目内容
(本题满分12分)
已知椭圆C: 的上顶点坐标为
的上顶点坐标为 ,离心率为
,离心率为 .
.
(Ⅰ)求椭圆方程;
(Ⅱ)设P为椭圆上一点,A为左顶点,F为椭圆的右焦点,求 的取值范围.
的取值范围.
(I)椭圆方程为 ;(Ⅱ)
;(Ⅱ) 的取值范围为
的取值范围为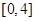 。
。
解析试题分析:解:(I)依题意得: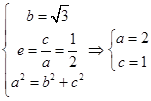 ,
,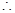 椭圆方程为
椭圆方程为
(Ⅱ)设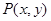 ,
,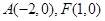 ,则
,则 ---(*)
---(*)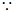 点
点 满足
满足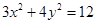 ,
,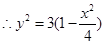 代入(*)式,得:
代入(*)式,得: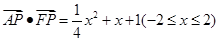
根据二次函数的单调性可得: 的取值范围为
的取值范围为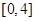
考点:本题主要考查椭圆方程的应用、平面向量数量积的运算等,涉及最值问题.
点评:最值问题解题的思路是先设出变量,表示出要求的表达式,结合圆锥曲线的方程,将其转化为只含一个变量的关系式,进而由不等式的性质或函数的最值进行计算.

练习册系列答案
相关题目
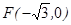 ,且过
,且过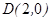 ,设点
,设点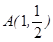 .
.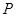 是椭圆上的动点,求线段
是椭圆上的动点,求线段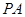 中点
中点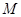 的轨迹方程。
的轨迹方程。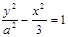 的焦点为F1,F2.离心率为2。
的焦点为F1,F2.离心率为2。 ,求线段AB中点M的轨迹方程,并说明轨迹是什么曲线。
,求线段AB中点M的轨迹方程,并说明轨迹是什么曲线。
 的离心率为
的离心率为 ,且椭圆上一点与椭圆的两个焦点构成的三角形周长为
,且椭圆上一点与椭圆的两个焦点构成的三角形周长为 .
. 的方程;
的方程; 与椭圆
与椭圆 两点,且以
两点,且以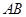 为直径的圆过椭圆的右顶点
为直径的圆过椭圆的右顶点 ,
, 面积的最大值.
面积的最大值.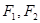 分别是椭圆的
分别是椭圆的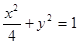 左,右焦点。
左,右焦点。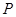 是第一象限内该椭圆上的一点,且
是第一象限内该椭圆上的一点,且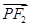 ·
·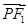 =
=
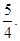 求点
求点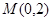 的直线与椭圆交于不同的两点
的直线与椭圆交于不同的两点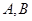 ,且
,且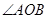 为锐角(其中O为坐标原点),求直线
为锐角(其中O为坐标原点),求直线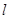 的斜率
的斜率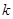 的取值范围。
的取值范围。 的离心率为2,坐标原点到
的离心率为2,坐标原点到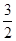 ,其中A
,其中A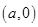 ,B
,B .
.  是双曲线虚轴在
是双曲线虚轴在 轴正半轴上的端点,过
轴正半轴上的端点,过 两点,求
两点,求 时,直线
时,直线 的方程.
的方程. 的左、右焦点分别是F1、F2,下顶点为A,线段OA的中点为B(O为坐标原点),如图.若抛物线C2:
的左、右焦点分别是F1、F2,下顶点为A,线段OA的中点为B(O为坐标原点),如图.若抛物线C2: 与
与 轴的交点为B,且经过F1,F2点.
轴的交点为B,且经过F1,F2点.
 ),N为抛物线C2上的一动点,过点N作抛物线C2的切线交椭圆C1于P、Q两点,求
),N为抛物线C2上的一动点,过点N作抛物线C2的切线交椭圆C1于P、Q两点,求 面积的最大值.
面积的最大值. 轴上的抛物线过点
轴上的抛物线过点 .
. 作直线交抛物线于
作直线交抛物线于 两点,使得
两点,使得 恰好平分线段
恰好平分线段 ,求直线
,求直线 均在椭圆
均在椭圆 上,直线
上,直线 分别过椭圆的左、右焦点
分别过椭圆的左、右焦点 当
当 时,有
时,有
 的方程
的方程 是椭圆
是椭圆 为圆
为圆 的任一条直径,求
的任一条直径,求 的最大值
的最大值