题目内容
(本小题16分)设双曲线: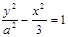 的焦点为F1,F2.离心率为2。
的焦点为F1,F2.离心率为2。
(1)求此双曲线渐近线L1,L2的方程;
(2)若A,B分别为L1,L2上的动点,且2 ,求线段AB中点M的轨迹方程,并说明轨迹是什么曲线。
,求线段AB中点M的轨迹方程,并说明轨迹是什么曲线。
(1)由已知双曲线的离心率为2得: 解得a2=1, ……2分
解得a2=1, ……2分
所以双曲线的方程为 , ……4分
, ……4分
所以渐近线L1,L2的方程为 和
和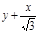 =0 ……6分
=0 ……6分
(2)c2=a2+b2=4,得c=2 ,所以 ,
,
又2 所以
所以 =10 ……8分
=10 ……8分
设A在L1上,B在L2上,设A(x1, ,B(x2,-
,B(x2,-
所以 即
即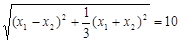 ……10分
……10分
设AB的中点M的坐标为(x,y),则x= ,y=
,y=
所以x1+x2=2x , x1-x2=2 y
y
所以 整理得:
整理得: ……14分
……14分
所以线段AB中点M的轨迹方程为: ,轨迹是椭圆。 ……16分
,轨迹是椭圆。 ……16分
解析试题分析:(1)由已知双曲线的离心率为2得: 解得a2=1, ……2分
解得a2=1, ……2分
所以双曲线的方程为 , ……4分
, ……4分
所以渐近线L1,L2的方程为 和
和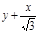 =0 ……6分
=0 ……6分
(2)c2=a2+b2=4,得c=2 ,所以 ,
,
又2 所以
所以 =10 ……8分
=10 ……8分
设A在L1上,B在L2上,设A(x1, ,B(x2,-
,B(x2,-
所以 即
即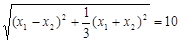 ……10分
……10分
设AB的中点M的坐标为(x,y),则x= ,y=
,y=
所以x1+x2=2x , x1-x2=2 y
y
所以 整理得:
整理得: ……14分
……14分
所以线段AB中点M的轨迹方程为: ,轨迹是椭圆。 ……16分
,轨迹是椭圆。 ……16分
考点:本题主要考查双曲线的标准方程及几何性质,轨迹方程的求法。
点评:点评:求曲线的轨迹方程是解析几何的基本问题,本题利用相关点法求轨迹方程,相关点法 根据相关点所满足的方程,通过转换而求动点的轨迹方程.中档题。

已知椭圆C: +
+ =1(a>b>0)的一个焦点是F(1,0),且离心率为
=1(a>b>0)的一个焦点是F(1,0),且离心率为 .
.
(Ⅰ)求椭圆C的方程;
(Ⅱ)设经过点F的直线交椭圆C于M,N两点,线段MN的垂直平分线交y轴于点P(0,y0),求y0的取值范围.
(本小题满分14分)设椭圆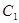 与抛物线
与抛物线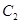 的焦点均在
的焦点均在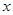 轴上,
轴上,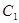 的中心和
的中心和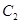 的顶点均为原点,从每条曲线上至少取两个点,将其坐标记录于下表中:
的顶点均为原点,从每条曲线上至少取两个点,将其坐标记录于下表中:
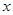 |  |  |  |  |  |
 |  |  |  |  |  |
1)求
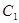 ,
,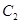 的标准方程, 并分别求出它们的离心率
的标准方程, 并分别求出它们的离心率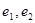 ;
;2)设直线
 与椭圆
与椭圆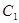 交于不同的两点
交于不同的两点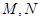 ,且
,且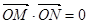 (其中
(其中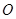 坐标原点),请问是否存在这样的直线
坐标原点),请问是否存在这样的直线 过抛物线
过抛物线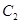 的焦点
的焦点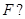 若存在,求出直线
若存在,求出直线 的方程;若不存在,请说明理由.
的方程;若不存在,请说明理由.  、
、 两个岛屿,
两个岛屿,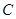 ,曾有渔船在距
,曾有渔船在距 轴,
轴,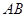 的垂直平分线为
的垂直平分线为 轴建立平面直角坐标系。
轴建立平面直角坐标系。
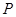 处反射信号的时间比为
处反射信号的时间比为 ,问你能否确定
,问你能否确定 的右焦点为F,上顶点为A,P为C
的右焦点为F,上顶点为A,P为C 上任一点,MN是圆
上任一点,MN是圆 的一条直径,若与AF平行且在y轴上的截距为
的一条直径,若与AF平行且在y轴上的截距为 的直线
的直线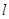 恰好与圆
恰好与圆 相切.
相切. 的离心率;
的离心率; 的最大值为49,求椭圆C
的最大值为49,求椭圆C 为圆上一动点,点
为圆上一动点,点 在
在 上,点
上,点 在
在 上,且满足
上,且满足 的轨迹为曲线
的轨迹为曲线 。
。
 求曲线
求曲线 若过定点F(0,2)的直线交曲线
若过定点F(0,2)的直线交曲线 (点
(点 在点
在点 之间),且满足
之间),且满足 ,求
,求 的取值范围。
的取值范围。 与直线
与直线 交于
交于 两点.
两点. 的长度;
的长度; 在抛物线
在抛物线 上,且
上,且 的面积为
的面积为 ,求点P的坐标.
,求点P的坐标. 的上顶点坐标为
的上顶点坐标为 ,离心率为
,离心率为 .
. 的取值范围.
的取值范围. 轴上的椭圆C的离心率为
轴上的椭圆C的离心率为 ,点A,B分别是椭圆C的长轴、短轴的端点,点O到直线AB的距离为
,点A,B分别是椭圆C的长轴、短轴的端点,点O到直线AB的距离为 。
。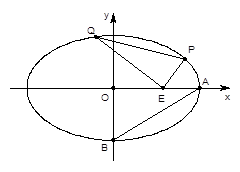
 的取值范围.
的取值范围.