题目内容
设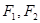 分别是椭圆的
分别是椭圆的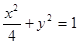 左,右焦点。
左,右焦点。
(1)若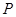 是第一象限内该椭圆上的一点,且
是第一象限内该椭圆上的一点,且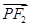 ·
·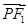 =
=
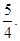 求点
求点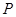 的坐标。
的坐标。
(2)设过定点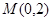 的直线与椭圆交于不同的两点
的直线与椭圆交于不同的两点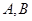 ,且
,且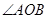 为锐角(其中O为坐标原点),求直线
为锐角(其中O为坐标原点),求直线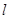 的斜率
的斜率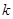 的取值范围。
的取值范围。
(1)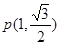 (2)
(2)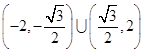
解析试题分析:(Ⅰ)易知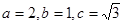 。
。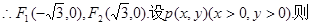
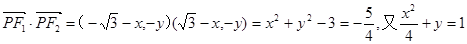 ,
,
………………………………3分
联立
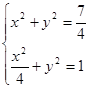 ,解得
,解得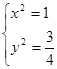
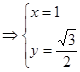 ,
,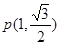 ………………5分
………………5分
(Ⅱ)显然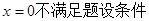 …………………………………………6分
…………………………………………6分
可设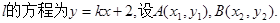
联立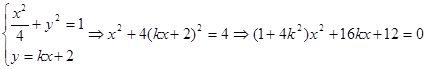
 ……………………………………7分
……………………………………7分
由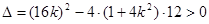
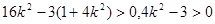
得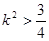 ① …………………………………………8分
① …………………………………………8分
又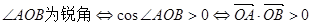 ,
,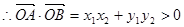 ………………………………………………9分
………………………………………………9分
又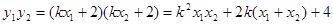
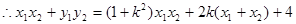
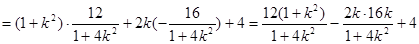
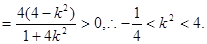 ② ……………………………………11分
② ……………………………………11分
综①②可知 …………12分
…………12分
考点:向量的坐标运算及直线与椭圆位置关系
点评:将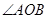 为锐角转化为
为锐角转化为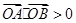

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
(本小题满分14分)设椭圆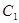 与抛物线
与抛物线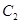 的焦点均在
的焦点均在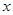 轴上,
轴上,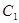 的中心和
的中心和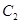 的顶点均为原点,从每条曲线上至少取两个点,将其坐标记录于下表中:
的顶点均为原点,从每条曲线上至少取两个点,将其坐标记录于下表中:
 |  |  |  |  |  |
 |  |  |  |  |  |
1)求
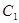 ,
,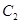 的标准方程, 并分别求出它们的离心率
的标准方程, 并分别求出它们的离心率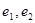 ;
;2)设直线
 与椭圆
与椭圆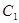 交于不同的两点
交于不同的两点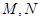 ,且
,且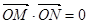 (其中
(其中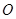 坐标原点),请问是否存在这样的直线
坐标原点),请问是否存在这样的直线 过抛物线
过抛物线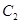 的焦点
的焦点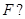 若存在,求出直线
若存在,求出直线 的方程;若不存在,请说明理由.
的方程;若不存在,请说明理由.  的顶点在坐标原点,它的准线经过双曲线
的顶点在坐标原点,它的准线经过双曲线 :
: 的左焦点
的左焦点 且垂直于
且垂直于 .
. 的坐标;
的坐标; .
. 与直线
与直线 交于
交于 两点.
两点. 的长度;
的长度; 在抛物线
在抛物线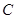 上,且
上,且 的面积为
的面积为 ,求点P的坐标.
,求点P的坐标. 过定点
过定点 ,且与直线
,且与直线 相切,椭圆
相切,椭圆 的对称轴为坐标轴,一个焦点是
的对称轴为坐标轴,一个焦点是 ,点
,点 在椭圆
在椭圆 的方程及其椭圆
的方程及其椭圆 与轨迹
与轨迹 处的切线平行,且直线
处的切线平行,且直线 两点,问:是否存在着这样的直线
两点,问:是否存在着这样的直线 的面积等于
的面积等于 ?如果存在,请求出直线
?如果存在,请求出直线 的上顶点坐标为
的上顶点坐标为 ,离心率为
,离心率为 .
. 的取值范围.
的取值范围. 以双曲线
以双曲线 的焦点为顶点,其离心率与双曲线的离心率互为倒数.
的焦点为顶点,其离心率与双曲线的离心率互为倒数. 的焦点为
的焦点为 ,准线为
,准线为 ,过
,过 ;
; 的值.
的值. 交于A,B两点.
交于A,B两点.