题目内容
(本题满分12分)设椭圆C1: 的左、右焦点分别是F1、F2,下顶点为A,线段OA的中点为B(O为坐标原点),如图.若抛物线C2:
的左、右焦点分别是F1、F2,下顶点为A,线段OA的中点为B(O为坐标原点),如图.若抛物线C2: 与
与 轴的交点为B,且经过F1,F2点.
轴的交点为B,且经过F1,F2点.
(Ⅰ)求椭圆C1的方程;
(Ⅱ)设M(0, ),N为抛物线C2上的一动点,过点N作抛物线C2的切线交椭圆C1于P、Q两点,求
),N为抛物线C2上的一动点,过点N作抛物线C2的切线交椭圆C1于P、Q两点,求 面积的最大值.
面积的最大值.
(Ⅰ)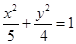 (Ⅱ)
(Ⅱ)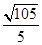
解析试题分析:(Ⅰ)解:由题意可知B(0,-1),则A(0,-2),故b=2.
令y=0得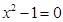 即
即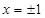 ,则F1(-1,0),F2(1,0),故c=1.
,则F1(-1,0),F2(1,0),故c=1.
所以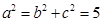 .于是椭圆C1的方程为
.于是椭圆C1的方程为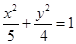 .…………4分
.…………4分
(Ⅱ)设N(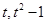 ),由于
),由于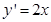 知直线PQ的方程为:
知直线PQ的方程为: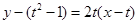 . 即
. 即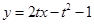 .……………………………5分
.……………………………5分
代入椭圆方程整理得: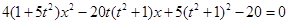 ,
,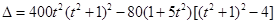 =
=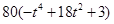 ,
,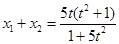 ,
, 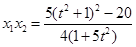 ,
,
故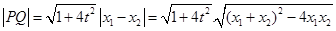
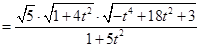 .………………………………7分
.………………………………7分
设点M到直线PQ的距离为d,则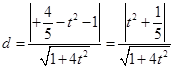 .…………………9分
.…………………9分
所以,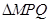 的面积S
的面积S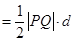
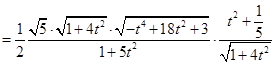
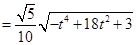
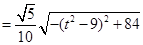
 ………………11分
………………11分
当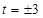 时取到“=”,经检验此时
时取到“=”,经检验此时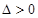 ,满足题意.
,满足题意.
综上可知,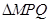 的面积的最大值为
的面积的最大值为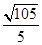 .…………………………12分
.…………………………12分
考点:椭圆标准方程及直线和椭圆的位置关系求最值
点评:本题计算量较大,要求学生有较强的数据处理能力

练习册系列答案
 全能测控期末小状元系列答案
全能测控期末小状元系列答案
相关题目
 、
、 两个岛屿,
两个岛屿, ,曾有渔船在距
,曾有渔船在距 轴,
轴,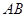 的垂直平分线为
的垂直平分线为 轴建立平面直角坐标系。
轴建立平面直角坐标系。
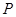 处反射信号的时间比为
处反射信号的时间比为 ,问你能否确定
,问你能否确定 与直线
与直线 交于
交于 两点.
两点. 的长度;
的长度; 在抛物线
在抛物线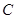 上,且
上,且 的面积为
的面积为 ,求点P的坐标.
,求点P的坐标. 的上顶点坐标为
的上顶点坐标为 ,离心率为
,离心率为 .
. 的取值范围.
的取值范围. 以双曲线
以双曲线 的焦点为顶点,其离心率与双曲线的离心率互为倒数.
的焦点为顶点,其离心率与双曲线的离心率互为倒数. 有相同的焦点,直线y=
有相同的焦点,直线y= 为
为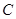 的一条渐近线.
的一条渐近线.  (0,4)的直线
(0,4)的直线 ,交双曲线
,交双曲线 点(
点(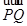 =
=
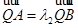 ,且
,且 时,求
时,求 的焦点为
的焦点为 ,准线为
,准线为 ,过
,过 ;
; 的值.
的值. 轴上的椭圆C的离心率为
轴上的椭圆C的离心率为 ,点A,B分别是椭圆C的长轴、短轴的端点,点O到直线AB的距离为
,点A,B分别是椭圆C的长轴、短轴的端点,点O到直线AB的距离为 。
。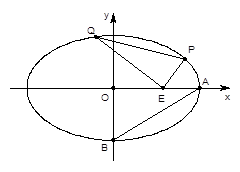
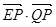 的取值范围.
的取值范围.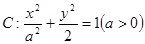 的左、右顶点分别为
的左、右顶点分别为 、
、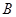 ,点
,点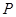 在椭圆上且异于
在椭圆上且异于 为坐标原点.
为坐标原点.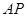 与
与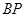 的斜率之积为
的斜率之积为 ,求椭圆的离心率;
,求椭圆的离心率; ,过点
,过点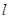 交
交 轴于点
轴于点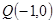 ,交
,交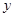 轴于点
轴于点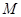 ,若
,若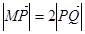 ,求直线
,求直线