题目内容
18.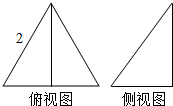 已知一个三棱锥的俯视图与侧(左)视图如图所示,俯视图是边长为2的正三角形,侧视图是有一条直角边为2的直角三角形,则该三棱锥的表面积为$\sqrt{19}+\sqrt{3}+2$.
已知一个三棱锥的俯视图与侧(左)视图如图所示,俯视图是边长为2的正三角形,侧视图是有一条直角边为2的直角三角形,则该三棱锥的表面积为$\sqrt{19}+\sqrt{3}+2$.
分析 由已知中的三视图,可知该几何体是一个以俯视图为底面的三棱锥,求出其各个面的面积,相加可得答案.
解答 解:由已知中的三视图,可知该几何体是一个以俯视图为底面的三棱锥,
其直观图如下所示: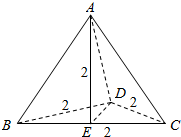
其中AE=BC=CD=BD=2,
则DE=$\sqrt{3}$,AB=AC=$\sqrt{5}$,AD=$\sqrt{7}$,
△ABC的面积为:$\frac{1}{2}$×2×2=2,
△BCD的面积为:$\frac{\sqrt{3}}{4}×{2}^{2}$=$\sqrt{3}$,
△ABD和△ACD的三边长分别为2,$\sqrt{5}$,$\sqrt{7}$,
则由海伦公式可得△ABD和△ACD的面积为:$\sqrt{\frac{2+\sqrt{5}+\sqrt{7}}{2}•\frac{-2+\sqrt{5}+\sqrt{7}}{2}•\frac{2-\sqrt{5}+\sqrt{7}}{2}\frac{2+\sqrt{5}-\sqrt{7}}{2}}$=$\frac{\sqrt{19}}{2}$
故该三棱锥的表面积为:$\sqrt{19}$+$\sqrt{3}$+2,
故答案为:$\sqrt{19}$+$\sqrt{3}$+2
点评 本题考查的知识点是由三视图求体积和表面积,解决本题的关键是得到该几何体的形状.

练习册系列答案
相关题目
9.下列叙述正确的是( )
| A. | 互斥事件一定不是对立事件,但是对立事件一定是互斥事件 | |
| B. | 若随机事件A发生的概率为P(A),则0<P(A)<1 | |
| C. | 频率是稳定的,概率是随机的 | |
| D. | 5张奖券中有一张有奖,甲先抽,乙后抽,那么乙比甲抽到有奖奖券的可能性小 |