题目内容
7.已知集合A={x∈R|ax2+2x+1=0},其中a∈R.(1)若1∈A,用列举法表示A;
(2)若A中有且仅有一个元素,求a的值组成的集合B.
分析 (1)若1∈A,则a=-3,解方程可用列举法表示A;
(2)若A中有且仅有一个元素,分a=0,和a≠0且△=0两种情况,分别求出满足条件a的值,可得集合B.
解答 解:(1)∵集合A={x∈R|ax2+2x+1=0},1∈A,
则a+2+1=0,解得a=-3,
则集合A={x∈R|-3x2+2x+1=0}={1,$-\frac{1}{3}$},
(2)当a=0时,A={x∈R|2x+1=0}有且仅有一个元素,
当a≠0时,若A中有且仅有一个元素,则方程ax2+2x+1=0的△=4-4a=0,解得a=1,
综上所述,a的值组成的集合B={0,1}
点评 本题考查的知识点是集合中元素与集合的关系,类一元二次方程根的个数与系数的关系,难度不大,属于基础题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
17.设等比数列{an}的前n项和为Sn,满足an>0,q>1,且a3+a5=20,a2a6=64,则S6等于( )
| A. | 63 | B. | 48 | C. | 42 | D. | 36 |
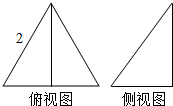 已知一个三棱锥的俯视图与侧(左)视图如图所示,俯视图是边长为2的正三角形,侧视图是有一条直角边为2的直角三角形,则该三棱锥的表面积为$\sqrt{19}+\sqrt{3}+2$.
已知一个三棱锥的俯视图与侧(左)视图如图所示,俯视图是边长为2的正三角形,侧视图是有一条直角边为2的直角三角形,则该三棱锥的表面积为$\sqrt{19}+\sqrt{3}+2$.