题目内容
15.已知(2x-1)20=a0+a1(x+1)+a2(x+1)2+…+a20(x+1)20(x∈R),则$\sum_{i=1}^{20}$i2ai=1480.分析 先换元,两边求导,20(2t-3)19=a1+2a2t+…+20a20t19,再两边同时乘以t,40t(2t-3)19=a1t+2a2t2+…+20a20t20,两边再求导,令t=1,可得$\sum_{i=1}^{20}$i2ai.
解答 解:令x+1=t,则x=t-1,
则(2t-3)20=a0+a1t+a2t2+…+a20t20(x∈R),
两边求导,40(2t-3)19=a1+2a2t+…+20a20t19,
两边同时乘以t,40t(2t-3)19=a1t+2a2t2+…+20a20t20,
两边再求导,40×(40t-3)(2t-3)18=a1+22a2t+…+202a20t19,
令t=1,可得$\sum_{i=1}^{20}$i2ai=40×37×(-1)18=1480,
故答案为:1480.
点评 本题考查二项式的系数和问题,考查导数知识的运用,正确转化是关键.

练习册系列答案
相关题目
7.已知f(x)=x|x|,若对任意的x≥1有f(x+m)+mf(x)<0恒成立,则实数m的取值范围是( )
| A. | (-∞,-1) | B. | (-∞,-1] | C. | (-∞,-2) | D. | (-∞,-2] |
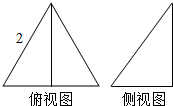 已知一个三棱锥的俯视图与侧(左)视图如图所示,俯视图是边长为2的正三角形,侧视图是有一条直角边为2的直角三角形,则该三棱锥的表面积为$\sqrt{19}+\sqrt{3}+2$.
已知一个三棱锥的俯视图与侧(左)视图如图所示,俯视图是边长为2的正三角形,侧视图是有一条直角边为2的直角三角形,则该三棱锥的表面积为$\sqrt{19}+\sqrt{3}+2$.