��Ŀ����
8����ֱ������ϵxOy�У���ԭ��OΪ���㣬��x��Ϊ������Ϊ���Ὠ��������ϵ����1�������ߦ�=cos��+1���cos��=1�Ĺ����㵽����ľ��룻
��2����ԲC�IJ�������Ϊ$\left\{\begin{array}{l}{x=acos��}\\{y=bsin��}\end{array}\right.$����Ϊ������a��b��0����ֱ��l��ԲO�ļ����귽�̷ֱ�Ϊ��sin����+$\frac{��}{4}$��=$\frac{\sqrt{2}}{2}$m��mΪ���㳣�������=b����ֱ��l������ԲC�Ľ��㣬����ԲO���У�����ԲC�������ʣ�
���� ��1��������=cos��+1���cos��=1�����ȼ�����æѣ���Ϊ�𰸣�
��2���ȸ��ݼ�������ֱ�������ת����ϵ��ֱ��l�ļ����귽�̷ֱ�Ϊ��sin����+$\frac{��}{4}$��=$\frac{\sqrt{2}}{2}$m��mΪ���㳣��������ֱ�����귽�̣�������ֱ��l������ԲC�Ľ��㣬����ԲO���У��Ӷ��õ�c=$\sqrt{2}$b����b2=a2-c2����ȥb��õ�����a��c�ĵ�ʽ�����������ԲC�������ʣ�
��� �⣺��1���ɦ�=cos��+1�ã�cos��=��-1�������cos��=1�æѣ���-1��=1��
��æ�=$\frac{\sqrt{5}+1}{2}$���=$\frac{1-\sqrt{5}}{2}$���ᣩ��
�����ߦ�=cos��+1���cos��=1�Ĺ����㵽����ľ���Ϊ$\frac{\sqrt{5}+1}{2}$��
��2��ֱ��l�ļ����귽�̷ֱ�Ϊ��sin����+$\frac{��}{4}$��=$\frac{\sqrt{2}}{2}$m��mΪ���㳣��������ֱ�����귽��Ϊx+y-m=0��
����x��Ľ�������Ϊ��m��0����������֪����m��0��Ϊ��Բ�Ľ��㣬��|m|=c��
��ֱ��l��ԲO����=b���У���$\frac{|-m|}{\sqrt{2}}$=b��
�Ӷ�c=$\sqrt{2}$b����b2=a2-c2��
��c2=2��a2-c2����
��3c2=2a2����$\frac{c}{a}=\frac{\sqrt{6}}{3}$��
����ԲC��������Ϊ$\frac{\sqrt{6}}{3}$��
���� ���⿼���������빫ʽ����������ֱ������Ļ�������������Բ�������ʣ������˲������̻�����ͨ���̣���ļ������ֱ������Ļ���������ѧ������������������������⣮

 �ظ���ʦ�㲦ϵ�д�
�ظ���ʦ�㲦ϵ�д�| A�� | ���ڵ㣨$\frac{5��}{12}$��0���Գ� | B�� | ����ֱ��x=$\frac{5��}{12}$�Գ� | ||
| C�� | ���ڵ㣨$\frac{��}{12}$��0���Գ� | D�� | ����ֱ��x=$\frac{��}{12}$�Գ� |
| A�� | ���⡰$a��b\;��\;��\frac{1}{a}��\frac{1}{b}$������������������ | |
| B�� | ���ں���y=f��x����x��R��y=|f��x��|��ͼ�����y��Գơ��ǡ�y=f��x�����溯�����ij�Ҫ���� | |
| C�� | ���Իع鷽��$\widehaty=\widehatbx+\widehata$��Ӧ��ֱ��һ���������������ݵ㣨x1��y1������x2��y2����������xn��yn���е�һ���� | |
| D�� | ���⡰$?{x_0}��R\;��\;x_0^2-{x_0}��0$���ķ��ǡ�?x��R��x2-x��0�� |
| A�� | ���е�ʵ��x����ʹx+$\frac{1}{x}$��2���� | |
| B�� | ����һ��ʵ��xʹ����ʽx2-2x+3��0���� | |
| C�� | ���x��y ��ʵ������ô��xy��0���ǡ�|x+y|=|x|+|y|���ij�ֵ�����Ҫ���� | |
| D�� | ����ף���a��b��c���ɵȲ����С��������ң���$\frac{a}{b}+\frac{c}{b}$=2���ij�Ҫ���� |
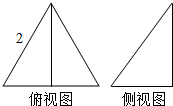 ��֪һ�������ĸ���ͼ��ࣨ����ͼ��ͼ��ʾ������ͼ�DZ߳�Ϊ2���������Σ�����ͼ����һ��ֱ�DZ�Ϊ2��ֱ�������Σ���������ı����Ϊ$\sqrt{19}+\sqrt{3}+2$��
��֪һ�������ĸ���ͼ��ࣨ����ͼ��ͼ��ʾ������ͼ�DZ߳�Ϊ2���������Σ�����ͼ����һ��ֱ�DZ�Ϊ2��ֱ�������Σ���������ı����Ϊ$\sqrt{19}+\sqrt{3}+2$��