题目内容
10.满足条件|g(x1)-g(x2)|≤4|x1-x2|的函数g(x)形成了一个集合M,其中x1,x2∈R,并且x12≤1,x22≤1,求函数y=f(x)=x2+3x-2(x∈R)与集合M的关系.分析 根据已知中满足条件|g(x1)-g(x2)|≤4|x1-x2|的函数g(x)形成了一个集合M,其中x1,x2∈R,并且x12,x22≤1,判断函数y=f(x)=x2+3x-2(x∈R)是否满足集合M的性质,可得结论.
解答 解:令g(x)=x2+3x-2,x12≤1,x22≤1,
则-1≤x1≤1,-1≤x2≤1,
则|g(x1)-g(x2)|=|(x12+3x1)-(x22+3x2)|=|(x1-x2)(x1+x2+3)|=|x1-x2||x1+x2+3|,
由1≤x1+x2+3≤5,
故|x1-x2|≤|g(x1)-g(x2)|≤5|x1-x2|,
故不满足|g(x1)-g(x2)|≤4|x1-x2|,
故函数y=f(x)=x2+3x-2(x∈R)∉集合M
点评 本题考查的知识点是二次函数的图象和性质,元素与集合的关系,难度中档.

练习册系列答案
相关题目
5.若x+y+z=0,则x3+y3+z3=( )
| A. | 0 | B. | x2y+y2z+z2x | C. | x2+y2+z2 | D. | 3xyz |
7.已知f(x)=x|x|,若对任意的x≥1有f(x+m)+mf(x)<0恒成立,则实数m的取值范围是( )
| A. | (-∞,-1) | B. | (-∞,-1] | C. | (-∞,-2) | D. | (-∞,-2] |
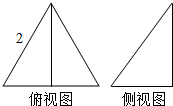 已知一个三棱锥的俯视图与侧(左)视图如图所示,俯视图是边长为2的正三角形,侧视图是有一条直角边为2的直角三角形,则该三棱锥的表面积为$\sqrt{19}+\sqrt{3}+2$.
已知一个三棱锥的俯视图与侧(左)视图如图所示,俯视图是边长为2的正三角形,侧视图是有一条直角边为2的直角三角形,则该三棱锥的表面积为$\sqrt{19}+\sqrt{3}+2$.