题目内容
【题目】已知奇函数f(x)![]() ,函数g(θ)=cos2θ+2sinθ
,函数g(θ)=cos2θ+2sinθ![]() ,θ∈[m,
,θ∈[m,![]() ].m,b∈R.
].m,b∈R.
(1)求b的值;
(2)判断函数f(x)在[0,1]上的单调性,并证明;
(3)当x∈[0,1]时,函数g(θ)的最小值恰为f(x)的最大值,求m的取值范围.
【答案】(1)b=0;(2)在[0,1]上的单调递增,证明见解析;(3)![]()
【解析】
(1)根据函数f(x)![]() 为奇函数,令f(0)=0求解.
为奇函数,令f(0)=0求解.
(2)函数f(x)在[0,1]上的单调递增,再利用函数的单调性定义证明.
(3)根据(2)知,函数f(x)在[0,1]上的单调递增,得到![]() .即g(θ)的最小值为
.即g(θ)的最小值为![]() ,再令t=sinθ,转化为二次函数求解.
,再令t=sinθ,转化为二次函数求解.
(1)因为函数f(x)![]() 为R上的奇函数,
为R上的奇函数,
所以f(0)=0,解得b=0.
(2)函数f(x)在[0,1]上的单调递增.
证明:设![]()
则:f(x2)﹣f(x1)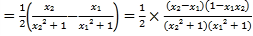 ,
,
因为![]() ,
,
所以x2﹣x1>0,1﹣x1x2>0,
所以![]() ,
,
即f(x2)![]() f(x1),
f(x1),
所以函数f(x)在[0,1]上的单调递增.
(3)由(2)得:函数f(x)在[0,1]上的单调递增,
所以![]() .所以g(θ)的最小值为
.所以g(θ)的最小值为![]() .
.
令t=sinθ,所以y![]() 的最小值为
的最小值为![]() ,
,
令![]()
解得![]()
所以![]() ,
,
即![]() ,
,
所以![]()
又因为θ∈[m,![]() ].m,b∈R,
].m,b∈R,
所以![]() .
.

【题目】为了检验两种不同的课堂教学模式对学生的成绩是否有影响,现从高二年级的甲(实行的“问题——探究式”)、乙(实行的“自学——指导式”)两个班中每班任意抽取20名学生进行测试,他们的成绩(总分150分)分布茎叶图如图所示(以十位百位为茎,个位为叶):

(1)若从参与测试的学生试卷中挑选2份卷面分数为90~100分的试着进行卷面分析,求抽取的2份试卷恰好每班1份的概率?
(2)记成绩在120分以上(包括120分)为优秀,其他的成绩为一般,请完成下面![]() 列联表,并分析是否有足够的把握(90%以上)认为这两种课堂教学模式对学生的成绩有影响?
列联表,并分析是否有足够的把握(90%以上)认为这两种课堂教学模式对学生的成绩有影响?
成绩 班级 | 优秀人数 | 一般人数 | 总计 |
甲班 | |||
乙班 | |||
总计 |
附: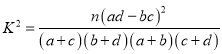
| 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
【题目】随着网络的发展,网上购物越来越受到人们的喜爱,各大购物网站为增加收入,促销策略越来越多样化,促销费用也不断增加,下表是某购物网站2018年1-8月促销费用(万元)和产品销量(万件)的具体数据:
月份 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
促销费用 | 2 | 3 | 6 | 10 | 13 | 21 | 15 | 18 |
产品销量 | 1 | 1 | 2 | 3 | 3.5 | 5 | 4 | 4.5 |
(1)根据数据绘制的散点图能够看出可用线性回归模型![]() 与
与![]() 的关系,请用相关系数
的关系,请用相关系数![]() 加以说明(系数精确到0.001);
加以说明(系数精确到0.001);
(2)建立![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() (系数精确到0.001);如果该公司计划在9月份实现产品销量超6万件,预测至少需要投入费用多少万元(结果精确到0.01).
(系数精确到0.001);如果该公司计划在9月份实现产品销量超6万件,预测至少需要投入费用多少万元(结果精确到0.01).
参考数据:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,其中
,其中![]() ,
,![]() 分别为第
分别为第![]() 个月的促销费用和产品销量,
个月的促销费用和产品销量,![]() .
.
参考公式:(1)样本![]() 相关系数
相关系数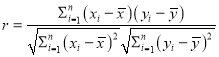 ;
;
(2)对于一组数据![]() ,
,![]() ,…,
,…,![]() ,其回归方程
,其回归方程![]() 的斜率和截距的最小二乘估计分别为
的斜率和截距的最小二乘估计分别为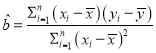 ,
,![]() .
.
