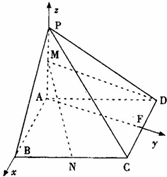
题目内容
已知三棱锥P-ABC中,PA⊥平面ABC,AB⊥AC,PA=AC=
AB=1,N为AB上一点,AB=4AN,M、S分别为PB、BC的中点.
(Ⅰ)求证:CM⊥SN;
(Ⅱ)求二面角P-CB-A的余弦值;
(Ⅲ)求直线SN与平面CMN所成角的大小.
| 1 |
| 2 |
(Ⅰ)求证:CM⊥SN;
(Ⅱ)求二面角P-CB-A的余弦值;
(Ⅲ)求直线SN与平面CMN所成角的大小.

(Ⅰ)证明:以A为原点,射线AB,AC,AP分别为x,y,z轴正向建立空间直角坐标系如图.
则P(0,0,1),C(0,1,0),B(2,0,0),
M(1,0,
),N(
,0,0),S(1,
,0),
=(1,-1,
),
=(-
,-
,0),
∵
?
=(1,-1,
)?(-
,-
,0)=0,
∴CM⊥SN.
(Ⅱ)设
=(0,0,1)为平面CBA的法向量,
=(2,-1,0),
=(0,1,-1),
设
=(x,y,z)为平面PCB的一个法向量
则
令x=1得
=(1,2,2,),
cos?<
,
>=
=
,
二面角P-CB-A的余弦值为
.
(Ⅲ)同理可得平面CMN的一个法向量
=(2,1,-2)
设直线SN与平面CMN所成角为θ,
∵sinθ=|cos<
,
>|=
,
∴SN与平面CMN所成角为45°.

则P(0,0,1),C(0,1,0),B(2,0,0),
M(1,0,
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| CM |
| 1 |
| 2 |
| SN |
| 1 |
| 2 |
| 1 |
| 2 |
∵
| CM |
| SN |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∴CM⊥SN.
(Ⅱ)设
| m |
| CB |
| PC |
设
| n |
则
|
| n |
cos?<
| m |
| n |
| ||||
|
| 2 |
| 3 |
二面角P-CB-A的余弦值为
| 2 |
| 3 |
(Ⅲ)同理可得平面CMN的一个法向量
| a |
设直线SN与平面CMN所成角为θ,
∵sinθ=|cos<
| SN |
| a |
| ||
| 2 |
∴SN与平面CMN所成角为45°.


练习册系列答案
相关题目
 中,
中, ,
, ,且
,且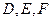 分别为
分别为 的中点.
的中点. ;
; 上是否存在一点
上是否存在一点 ,使得
,使得 ∥平面
∥平面 ?证明
?证明 你的结论.
你的结论.