题目内容
10.命题p:关于x的方程x|x|-2x+m=0(m∈R)有三个实数根;命题q:0≤m<1;则命题p成立是命题q成立的( )| A. | 充分而不必要的条件 | B. | 必要而不充分的条件 | ||
| C. | 充要条件 | D. | 既不充分又不必要的条件 |
分析 根据充分条件和必要条件的定义结合函数和方程之间的关系进行判断即可.
解答 解:由方程 $x|x|-2x+m=0⇒m=x(2-|x|)=\left\{\begin{array}{l}x(2-x),x≥0\\ x(2+x),x<0\end{array}\right.$,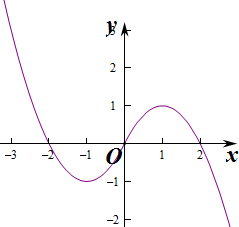
易知函数f(x)是R上的奇函数,由f(x)的图象可知,函数f(x)在[0,+∞)上的最大值是1,
根据图象的对称性知函数f(x)在(-∞,0)上的最小值为-1,
又函数f(x)的图象与x轴有3个交点,
那么原方程有3个实数根的充要条件是(-1,1),而[0,1)?(-1,1),
故选:B
点评 本题主要考查充分条件和必要条件的判断,以及函数与方程之间的关系,利用数形结合是解决本题的关键.

练习册系列答案
相关题目
1.某天下午要排物理、化学、生物和两节自习共5节课,如果第一节不排生物,最后一节不排物理,那么不同的排法共有( )
| A. | 36种 | B. | 39种 | C. | 60种 | D. | 78种 |
18.设集合M={x∈R|x2+x-6<0},N={x∈R||x-1|≤2}.则M∩N=( )
| A. | (-3,-2] | B. | [-2,-1) | C. | [-1,2) | D. | [2,3) |
2.设等差数列{an}和等比数列{bn}首项都是1,公差和公比都是2,则a${\;}_{{b}_{2}}$+a${\;}_{{b}_{3}}$+a${\;}_{{b}_{4}}$=( )
| A. | 24 | B. | 25 | C. | 26 | D. | 27 |
19.函数f(x)=ln(x-2x2)的定义域为( )
| A. | (-∞,0)∪($\frac{1}{2}$,+∞) | B. | [0,$\frac{1}{2}$] | C. | (0,$\frac{1}{2}$ ) | D. | (-∞,0]∪[$\frac{1}{2}$,+∞) |
 如图,三棱锥C-ABD中,AB=AD=BD=BC=CD=2,O为BD的中点,∠AOC=120°,P为AC上一点,Q为AO上一点,且$\frac{AP}{PC}$=$\frac{AQ}{QO}$=2.
如图,三棱锥C-ABD中,AB=AD=BD=BC=CD=2,O为BD的中点,∠AOC=120°,P为AC上一点,Q为AO上一点,且$\frac{AP}{PC}$=$\frac{AQ}{QO}$=2.