题目内容
是否存在这样的实数a,使函数f(x)=x2+(3a-2)x+a-1在区间[-1,3]上恒有一个零点,且只有一个零点?若存在,求出a的取值范围;若不存在,说明理由.
a的取值范围为a>1或a<-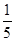
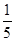
解:令f(x)=0,则Δ=(3a-2)2-4(a-1)=9a2-16a+8=9(a- )2+
)2+ >0,即f(x)=0有两个不相等的实数根,
>0,即f(x)=0有两个不相等的实数根,
∴若实数a满足条件,则只需f(-1)·f(3)≤0即可.
f(-1)·f(3)=(1-3a+2+a-1)·(9+9a-6+a-1)=4(1-a)(5a+1)≤0,
∴a≤-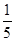 或a≥1.
或a≥1.
检验:(1)当f(-1)=0时,a=1,所以f(x)=x2+x.
令f(x)=0,即x2+x=0,得x=0或x=-1.
方程在[-1,3]上有两个实数根,不合题意,故a≠1.
当f(3)=0时,a=-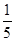 ,
,
此时f(x)=x2- x-
x-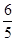 .
.
令f(x)=0,即x2- x-
x-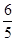 =0,
=0,
解得x=- 或x=3.
或x=3.
方程在[-1,3]上有两个实数根,不合题意,故a≠-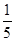 .
.
所以a的取值范围为a>1或a<-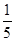 .
.
 )2+
)2+ >0,即f(x)=0有两个不相等的实数根,
>0,即f(x)=0有两个不相等的实数根,∴若实数a满足条件,则只需f(-1)·f(3)≤0即可.
f(-1)·f(3)=(1-3a+2+a-1)·(9+9a-6+a-1)=4(1-a)(5a+1)≤0,
∴a≤-
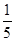 或a≥1.
或a≥1.检验:(1)当f(-1)=0时,a=1,所以f(x)=x2+x.
令f(x)=0,即x2+x=0,得x=0或x=-1.
方程在[-1,3]上有两个实数根,不合题意,故a≠1.
当f(3)=0时,a=-
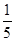 ,
,此时f(x)=x2-
 x-
x-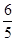 .
.令f(x)=0,即x2-
 x-
x-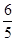 =0,
=0,解得x=-
 或x=3.
或x=3.方程在[-1,3]上有两个实数根,不合题意,故a≠-
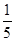 .
.所以a的取值范围为a>1或a<-
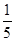 .
.
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 ,
,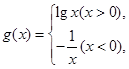 则函数
则函数 在区间
在区间 内的零点个数为( )
内的零点个数为( )



 、
、 、
、 满足
满足 ,
, ,则
,则 (x>0).
(x>0).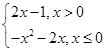 若函数g(x)=f(x)-m有3个零点,则实数m的取值范围是________.
若函数g(x)=f(x)-m有3个零点,则实数m的取值范围是________. ,若函数g(x)=f(x)-k有两个零点,则实数k的取值范围是________.
,若函数g(x)=f(x)-k有两个零点,则实数k的取值范围是________.