题目内容
函数f(x)＝lnx－x－a有两个不同的零点，则实数a的取值范围是( )
| A．(－∞，－1] | B．(－∞，－1) |
| C．[－1，＋∞) | D．(－1，＋∞) |
B
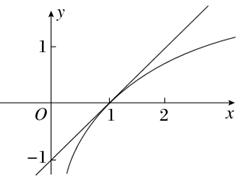
函数f(x)＝lnx－x－a的零点，即为关于x的方程lnx－x－a＝0的实根，将方程lnx－x－a＝0，化为方程lnx＝x＋a，令y1＝lnx，y2＝x＋a，由导数知识可知，直线y2＝x＋a与曲线y1＝lnx相切时有a＝－1，若关于x的方程lnx－x－a＝0有两个不同的实根，则实数a的取值范围是(－∞，－1)．故选B．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
有极值点
，且
，则关于
的方程
的不同实根的个数是（ ）
，4)
)
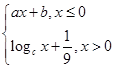的图象如图所示，则a＋b＋c＝________.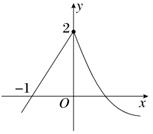
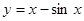的零点个数是