题目内容
有一枚正方体骰子,六个面分别写1、2、3、4、5、6的数字,规定“抛掷该枚骰子得到的数字是抛掷后,面向上的那一个数字”.已知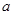 和
和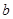 是先后抛掷该枚骰子得到的数字,函数
是先后抛掷该枚骰子得到的数字,函数
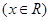
(1)若先抛掷骰子得到的数字是3,求再次抛掷骰子时,使函数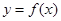 有零点的概率;
有零点的概率;
(2)求函数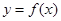 在区间(-3,+∞)上是增函数的概率.
在区间(-3,+∞)上是增函数的概率.
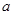 和
和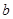 是先后抛掷该枚骰子得到的数字,函数
是先后抛掷该枚骰子得到的数字,函数
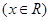
(1)若先抛掷骰子得到的数字是3,求再次抛掷骰子时,使函数
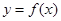 有零点的概率;
有零点的概率;(2)求函数
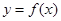 在区间(-3,+∞)上是增函数的概率.
在区间(-3,+∞)上是增函数的概率.(1)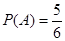 (2)
(2)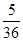
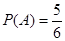 (2)
(2)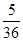
试题分析:(1)解:设事件A:再次抛掷骰子时,函数
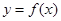 有零点.
有零点.若
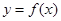 有零点,则
有零点,则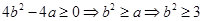
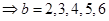 .所以
.所以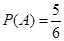 .
.答:再次抛掷骰子时,函数
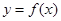 有零点的概率为
有零点的概率为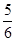 .
. (2)解:设事件B为函数
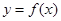 在
在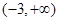 为增函数.
为增函数.若函数
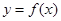 在
在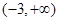 上是增函数,则有
上是增函数,则有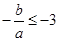 ,即
,即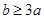 .
. 当
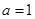 时,
时,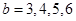 ;当
;当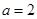 时,
时,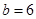 .所以
.所以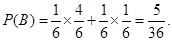
答:函数
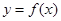 在
在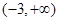 上是增函数的概率是
上是增函数的概率是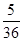 .
. 点评:本题巧妙地把概率、不等式组、二次函数等知识结合在一起,出题思路新颖,别具-格.有利于考查学生灵活应用基础知识解决问题的能力.用到的知识点为:概率=所求情况数与总情况数之比.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
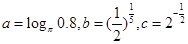 ,则有( )
,则有( )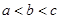
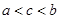
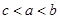

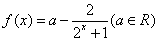
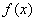 的单调性;
的单调性;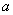 ,使函数
,使函数 ,
,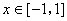 ,则
,则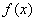 为偶函数,且在
为偶函数,且在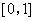 上单调递减
上单调递减 上单调递增
上单调递增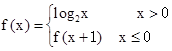 ,则
,则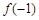 =( )
=( )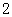
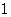
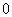

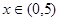 时,函数
时,函数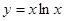 的单调性
的单调性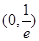 上单调递减,在
上单调递减,在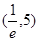 上单调递增
上单调递增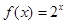 和
和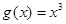 的图像如图所示,设两函数的图像交于点
的图像如图所示,设两函数的图像交于点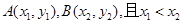 .
.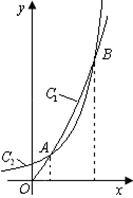
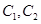 分别对应哪一个函数?
分别对应哪一个函数?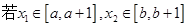 ,且
,且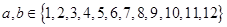 ,指出
,指出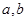 的值,并说明理由;
的值,并说明理由;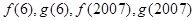
 在下列定义域内的值域。
在下列定义域内的值域。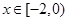 函数y=f(x)的值域
函数y=f(x)的值域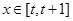 (其中
(其中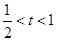 )函数y=f(x)的值域。
)函数y=f(x)的值域。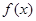 的导函数为
的导函数为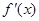 ,且满足
,且满足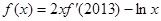 ,则
,则 ( )
( )