题目内容
【题目】已知各项均为正数的数列![]() 满足
满足![]() , 且
, 且![]() ,其中
,其中![]() .
.
(1) 求数列![]() 的通项公式;
的通项公式;
(2) 设数列{bn}满足 bn=![]() ,是否存在正整数
,是否存在正整数![]() ,使得b1,bm,bn成等比数列?若存在,求出所有的
,使得b1,bm,bn成等比数列?若存在,求出所有的![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
(3) 令![]() ,记数列{cn}的前
,记数列{cn}的前![]() 项和为
项和为![]() ,其中
,其中![]() ,证明:
,证明:![]() .
.
【答案】(1)![]() (2)存在,
(2)存在,![]() (3)证明见解析
(3)证明见解析
【解析】分析:(1)由已知条件推导出数列{an}是公比为2的等比数列.由此能求出![]() ,n∈N*.
,n∈N*.
(2)![]() =
=![]() ,若b1,bm,bn成等比数列,则
,若b1,bm,bn成等比数列,则![]() .由此能求出当且仅当m=2,n=12.使得b1,bm,bn成等比数列.
.由此能求出当且仅当m=2,n=12.使得b1,bm,bn成等比数列.
(3)![]() =
=![]() [
[![]() ],由此利用裂项求和法能证明
],由此利用裂项求和法能证明![]() .
.
详解:(1)解:∵an+12=2an2+anan+1,∴(an+1+an)(2an﹣an+1)=0,
又an>0,∴2an﹣an+1=0,即2an=an+1,
∴数列{an}是公比为2的等比数列.
由a2+a4=2a3+4,得2a1+8a1=8a1+4,解得a1=2.
∴数列{an}的通项公式为![]() ,n∈N*.
,n∈N*.
(2)解:![]() =
=![]() ,若b1,bm,bn成等比数列,则(
,若b1,bm,bn成等比数列,则(![]() )2=
)2=![]() ,
,
即![]() .
.
由![]() ,得
,得![]() ,
,
∴﹣2m2+4m+1>0,解得:1﹣![]() .
.
又m∈N*,且m>1,∴m=2,此时n=12.
故当且仅当m=2,n=12.使得b1,bm,bn成等比数列.
(3)证明:![]() =
=![]()
=![]() [
[![]() ]
]
=![]() [
[![]() ],
],
∴![]() [
[![]() ]
]
=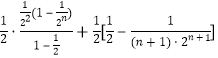
=![]() ,
,
∵(![]() )n+1
)n+1![]() 递减,
递减,
∴0<(![]() )n+1
)n+1![]() ≤
≤![]()
∴![]() ,∴
,∴![]() .
.

练习册系列答案
 步步高口算题卡系列答案
步步高口算题卡系列答案 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案 小学教材完全解读系列答案
小学教材完全解读系列答案
相关题目