题目内容
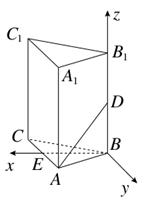
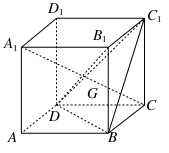
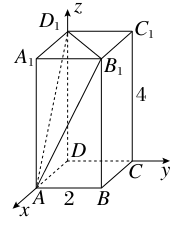
在正三棱柱ABC-A1B1C1中,已知AB=1,D在棱BB1上,且BD=1,则AD与平面AA1C1C所成的角的正弦值为( )
A.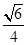 | B.-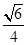 | C.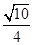 | D.-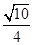 |

A
取AC中点E,连接BE,则BE⊥AC,
如图,建立空间直角坐标系B-xyz,
则A(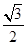 ,
,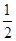 ,0),D(0,0,1),
,0),D(0,0,1),
则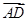 =(-
=(-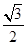 ,-
,-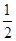 ,1).
,1).
∵平面ABC⊥平面AA1C1C,BE⊥AC,
∴BE⊥平面AA1C1C.
∴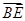 =(
=(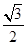 ,0,0)为平面AA1C1C的一个法向量,
,0,0)为平面AA1C1C的一个法向量,
∴cos〈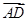 ,
,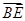 〉=-
〉=-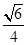 ,
,
设AD与平面AA1C1C所成的角为α,
∴sinα=|cos〈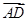 ,
,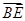 〉|=
〉|=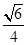 ,故选A.
,故选A.
如图,建立空间直角坐标系B-xyz,
则A(
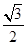 ,
,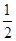 ,0),D(0,0,1),
,0),D(0,0,1),则
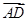 =(-
=(-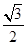 ,-
,-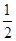 ,1).
,1).∵平面ABC⊥平面AA1C1C,BE⊥AC,
∴BE⊥平面AA1C1C.
∴
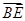 =(
=(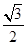 ,0,0)为平面AA1C1C的一个法向量,
,0,0)为平面AA1C1C的一个法向量,∴cos〈
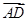 ,
,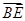 〉=-
〉=-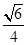 ,
,设AD与平面AA1C1C所成的角为α,
∴sinα=|cos〈
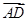 ,
,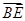 〉|=
〉|=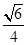 ,故选A.
,故选A.
练习册系列答案
相关题目
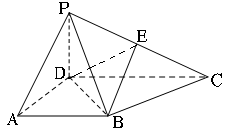
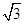 ,求三棱锥E-ACD的体积.
,求三棱锥E-ACD的体积.

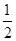
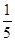

 分别是
分别是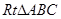 的斜边
的斜边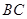 上的两个三等分点,已知
上的两个三等分点,已知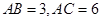 ,则
,则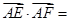 .
.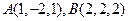 ,点
,点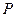 在
在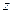 轴上,且
轴上,且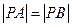 ,则点
,则点