题目内容
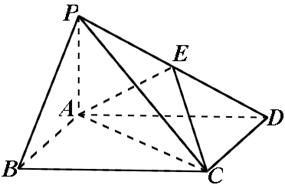
如图，四棱锥P-ABCD中，底面ABCD为矩形，PA⊥平面ABCD，E为PD的中点.
（1）证明：PB∥平面AEC；
（2）设二面角D-AE-C为60°，AP=1，AD=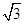
，求三棱锥E-ACD的体积.
（1）证明：PB∥平面AEC；
（2）设二面角D-AE-C为60°，AP=1，AD=
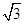，求三棱锥E-ACD的体积.
试题分析：本题第（1）问，证明直线与平面平行，可利用线面平行的判定定理来证明；对第（2）问，可先建立空间直角坐标系，由空间向量的坐标运算计算二面角，从而计算出AB，然后由棱锥的体积公式求出三棱锥的体积.
试题解析：（1）证明：设O为AC与BD交点，连结OE，则由矩形ABCD知：O为BD的中点，因为E是BD的中点，所以OE∥PB，因为OE
面AEC，PB
面AEC，所以PB∥平面AEC。
（2）以A为原点，直线AB、AD、AP分别为x、y、z轴建立空间直角坐标系，设AB=m，则
是平面AED的一个法向量，设
是平面AEC的法向量，则
，解得
，
，所以令
，得
，所以
=
，因为二面角的大小与其两个半平面的两个法向量的夹角相等哉互补，所以=
，解得
，因为E是PD的中点，所以三棱锥E-ACD的高为
，所以三棱锥E-ACD的体积为
=
=
.
【易错点】对第（1）问，证明线面平行时,容易漏掉条件；对第（2）问，二面角的大小与两个法向量夹角相等或互补的关系，一部分同学容易得出它们相等；并且计算法向量可能出现错误.
试题解析：（1）证明：设O为AC与BD交点，连结OE，则由矩形ABCD知：O为BD的中点，因为E是BD的中点，所以OE∥PB，因为OE
面AEC，PB面AEC，所以PB∥平面AEC。（2）以A为原点，直线AB、AD、AP分别为x、y、z轴建立空间直角坐标系，设AB=m，则
是平面AED的一个法向量，设是平面AEC的法向量，则，解得，，所以令，得，所以=，因为二面角的大小与其两个半平面的两个法向量的夹角相等哉互补，所以=，解得，因为E是PD的中点，所以三棱锥E-ACD的高为，所以三棱锥E-ACD的体积为==.【易错点】对第（1）问，证明线面平行时,容易漏掉条件；对第（2）问，二面角的大小与两个法向量夹角相等或互补的关系，一部分同学容易得出它们相等；并且计算法向量可能出现错误.
练习册系列答案
优学名师名题系列答案
相关题目
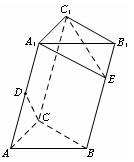
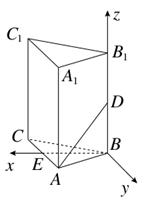
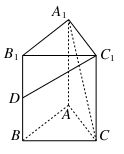
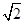a，A1C=CA=AB=a，AB⊥AC，D为AA1中点.
.
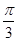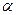内，其余顶点在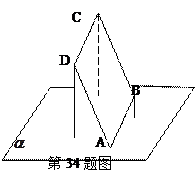
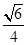
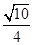
中，一个四面体的顶点坐标分别是（0,0,2），（2,2,0），（1,2，1），（2,2,2），给出编号①、②、③、④的四个图，则该四面体的正视图和俯视图分别为（ ）
＝
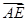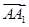＋x
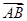＋y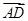
，则x、y的值分别为( )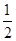
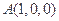的距离除以到
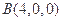的距离的值为
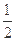的点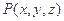
的坐标满足( )
