题目内容
18.已知A(2,0),B(3,3),直线l∥AB,则直线l的斜率为( )| A. | -3 | B. | 3 | C. | -$\frac{1}{3}$ | D. | $\frac{1}{3}$ |
分析 由于直线l∥AB,可得kl=kAB.再利用斜率计算公式即可得出.
解答 解:kAB=$\frac{3-0}{3-2}$=3,
∵直线l∥AB,
∴kl=kAB=3.
故选:B.
点评 本题考查了斜率计算公式、相互平行的直线斜率之间的关系,属于基础题.

练习册系列答案
相关题目
8.在(1+x)n的展开式中,第9项为( )
| A. | C${\;}_{n}^{9}$x9 | B. | C${\;}_{n}^{8}$x8 | C. | C${\;}_{n}^{9}$xn-9 | D. | C${\;}_{n}^{8}$xn-8 |
10.已知直线l的方程x=a,a∈R,分别交曲线y=πsinx和y=πcosx不同的两点M,N,则线段|MN|的取值范围是( )
| A. | [0,π] | B. | [0,$\sqrt{2}$π] | C. | [0,$\sqrt{3}π$] | D. | [0,2π] |
7.已知数列{an},{bn}满足:a1b1+a2b2+a3b3+…+anbn=(n-1)•2n+1+2(n∈N*),若{bn}是首项为1,公比为2的等比数列,则数列{an}的通项公式是( )
| A. | an=2n-1 | B. | an=2n | C. | an=2n | D. | an=2n-1 |
5.A,B,C为空间三点,经过这三点( )
| A. | 能确定一个平面或不能确定平面 | B. | 可以确定一个平面 | ||
| C. | 能确定无数个平面 | D. | 能确定一个或无数个平面 |
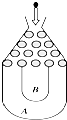 将一个半径适当的小球放入如图所示的容器最上方的入口处,小球自由下落,小球在下落的过程中,将遇到黑色障碍物3次,最后落入A袋或B袋中.已知小球每次遇到障碍物时,向左、右两边下落的概率分别是p,1-p.
将一个半径适当的小球放入如图所示的容器最上方的入口处,小球自由下落,小球在下落的过程中,将遇到黑色障碍物3次,最后落入A袋或B袋中.已知小球每次遇到障碍物时,向左、右两边下落的概率分别是p,1-p.