题目内容
3．若圆柱OO′的底面半径与高均为1，则其表面积为4π．分析 根据已知中圆柱的底面半径及高，代入圆柱表面积公式S=2πr（r+h）可得答案
解答 解：∵圆柱OO′的底面半径与高均为1，
即r=h=1，
故圆柱的表面积S=2πr（r+h）=4π，
故答案为：4π
点评 本题考查的知识点是旋转体，圆柱的表面积，熟练掌握圆柱的表面积公式，是解答的关键．
练习册系列答案
相关题目
14．抛掷一枚均匀硬币两次，已知有一次是正面向上，则另一次正面向上的概率为（ ）
| A． | $\frac{1}{2}$ | B． | $\frac{1}{4}$ | C． | $\frac{1}{3}$ | D． | $\frac{2}{3}$ |
11．定义在上（0，$\frac{π}{4}$）的函数f（x）满足2f（x）＜f′（x）tan2x，f′（x）是f（x）的导函数，则（ ）
| A． | $\sqrt{3}$f（$\frac{π}{12}$）＜f（$\frac{π}{6}$） | B． | f（$\frac{1}{4}$）$＞2f（\frac{π}{12}）$sin$\frac{1}{2}$ | C． | $\sqrt{3}$f（$\frac{π}{8}$）＞$\sqrt{2}$f（$\frac{π}{6}$） | D． | $\sqrt{2}$f（$\frac{π}{12}$）＞f（$\frac{π}{8}$） |
18．已知A（2，0），B（3，3），直线l∥AB，则直线l的斜率为（ ）
| A． | -3 | B． | 3 | C． | -$\frac{1}{3}$ | D． | $\frac{1}{3}$ |
8．已知角α的终边与圆x2+y2=4相交于点P（1，-$\sqrt{3}$），则sinα的值为（ ）
| A． | -$\frac{\sqrt{3}}{2}$ | B． | -$\frac{1}{2}$ | C． | $\frac{1}{2}$ | D． | $\frac{\sqrt{3}}{2}$ |
15．直线x+1=0的倾斜角为（ ）
| A． | 0 | B． | $\frac{π}{4}$ | C． | $\frac{π}{2}$ | D． | $\frac{3π}{4}$ |
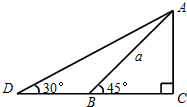如图，有一条长为a米的斜坡AB，它的坡角为45°，现保持坡高AC不变，将坡角改为30°，则斜坡AD的长为$\sqrt{2}$a米．
10．函数y=x4-2x2+5的单调减区间为（ ）
| A． | （-∞，-1）及（0，1） | B． | （-1，0）及（1，+∞） | C． | （-1，1） | D． | （-∞，-1）及（1，+∞） |