题目内容
7.已知数列{an},{bn}满足:a1b1+a2b2+a3b3+…+anbn=(n-1)•2n+1+2(n∈N*),若{bn}是首项为1,公比为2的等比数列,则数列{an}的通项公式是( )| A. | an=2n-1 | B. | an=2n | C. | an=2n | D. | an=2n-1 |
分析 通过将bn=2n-1代入a1b1+a2b2+a3b3+…+anbn=a1+2a2+22a3+…+2n-1an,利用2n-1an=(n-1)•2n+1-(n-2)•2n计算即可.
解答 解:∵数列{bn}是首项为1,公比为2的等比数列,
∴bn=2n-1,
∴a1b1+a2b2+a3b3+…+anbn=a1+2a2+22a3+…+2n-1an=(n-1)•2n+1+2,
∴a1+2a2+22a3+…+2n-2an-1=(n-1-1)•2n+1-1+2(n≥2),
两式相减得:2n-1an=(n-1)•2n+1-(n-2)•2n=n•2n,
∴an=$\frac{n•{2}^{n}}{{2}^{n-1}}$=2n,
当n=1时,a1b1=2,
即a1=2满足上式,
∴数列{an}的通项公式是an=2n,
故选:C.
点评 本题考查等差数列,注意解题方法的积累,属于基础题.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案
相关题目
17.M(x0,y0)为圆x2+y2=a2(a>0)内异于圆心的一点,则直线x•x0+y•y0=a2与该圆的位置关系为( )
| A. | 相离 | B. | 相交 | C. | 相切 | D. | 相切或相离 |
18.已知A(2,0),B(3,3),直线l∥AB,则直线l的斜率为( )
| A. | -3 | B. | 3 | C. | -$\frac{1}{3}$ | D. | $\frac{1}{3}$ |
15.直线x+1=0的倾斜角为( )
| A. | 0 | B. | $\frac{π}{4}$ | C. | $\frac{π}{2}$ | D. | $\frac{3π}{4}$ |
19.已知命题p:?a0∈(0,+∞),a02-2a0-3>0,那么命题p的否定是( )
| A. | ?a0∈(0,+∞),a02-2a0-3≤0 | B. | ?a0∈(-∞,0),a02-2a0-3≤0 | ||
| C. | ?a∈(0,+∞),a2-2a-3≤0 | D. | ?a∈(-∞,0),a2-2a-3≤0 |
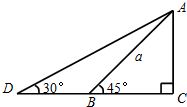 如图,有一条长为a米的斜坡AB,它的坡角为45°,现保持坡高AC不变,将坡角改为30°,则斜坡AD的长为$\sqrt{2}$a米.
如图,有一条长为a米的斜坡AB,它的坡角为45°,现保持坡高AC不变,将坡角改为30°,则斜坡AD的长为$\sqrt{2}$a米.