题目内容
3.在△ABC中,若sin(C-B)=1,sinA=$\frac{1}{3}$,BC=$\sqrt{6}$,则△ABC的面积为3$\sqrt{2}$.分析 由sin(C-B)=1,B,C∈(0,π).可得C-B=$\frac{π}{2}$.可知B为锐角.由于sinA=$\frac{1}{3}$,可得sin(B+C)=$\frac{1}{3}$,再利用倍角公式可得cosB,sinB.sinC=$sin(B+\frac{π}{2})$=cosB=$\frac{\sqrt{6}}{3}$.
再利用正弦定理可得b,c,再利用三角形面积计算公式即可得出.
解答 解:∵sin(C-B)=1,B,C∈(0,π).
∴C-B=$\frac{π}{2}$.可知B为锐角.
∵sinA=$\frac{1}{3}$,
∴sin(B+C)=$\frac{1}{3}$,
∴$sin(2B+\frac{π}{2})$=$\frac{1}{3}$,
∴$\frac{1}{3}$=cos2B=2cos2B-1,
解得cosB=$\frac{\sqrt{6}}{3}$.
∴sinB=$\frac{\sqrt{3}}{3}$.sinC=$sin(B+\frac{π}{2})$=cosB=$\frac{\sqrt{6}}{3}$.
由正弦定理可得:$\frac{a}{sinA}=\frac{b}{sinB}$=$\frac{c}{sinC}$,
∴b=$\frac{asinB}{sinA}$=$\frac{\sqrt{6}×\frac{\sqrt{3}}{3}}{\frac{1}{3}}$=3$\sqrt{2}$,
c=$\frac{asinC}{sinA}$=$\frac{\sqrt{6}×\frac{\sqrt{6}}{3}}{\frac{1}{3}}$=6.
∴S△ABC=$\frac{1}{2}bcsinA$=$\frac{1}{2}×3\sqrt{2}×6×\frac{1}{3}$=3$\sqrt{2}$.
故答案为:3$\sqrt{2}$.
点评 本题考查了正弦定理、三角形面积计算公式、倍角公式,考查了推理能力与计算能力,属于中档题.

 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案| A. | -2 | B. | $\frac{2}{3}$ | C. | $\frac{1}{3}$ | D. | 1 |
| A. | $\left\{\begin{array}{l}{x-2>0}\\{x+1<0}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{x-2<0}\\{x+1>0}\end{array}\right.$ | C. | (x-2)(x+1)<0 | D. | (x-2)(x+1)>0 |
| A. | 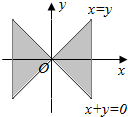 | B. | 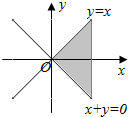 | C. | 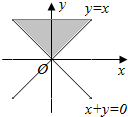 | D. | 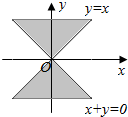 |