题目内容
下面四图都是在同一坐标系中某三次函数及其导函数的图像,其中一定不正确的序号是( )
| A.①② | B.③④ | C.①③ | D.①④ |
B
解析试题分析:解:由图象可知,在图①、②在每个区间上函数的单调性与对应的导数的符号是正确的,即单调增区间导数大于零,单调减区间上导数小于零;在③中显示在区间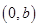 上导函数的值为负值,而该区间上的函数图象显示不单调,二者不一致,所以③不正确;在④图象显示在区间
上导函数的值为负值,而该区间上的函数图象显示不单调,二者不一致,所以③不正确;在④图象显示在区间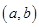 上导函数的值总为正数,而相应区间上的函数图象却显示为减函数,二者相矛盾,所以不正确.故选B.
上导函数的值总为正数,而相应区间上的函数图象却显示为减函数,二者相矛盾,所以不正确.故选B.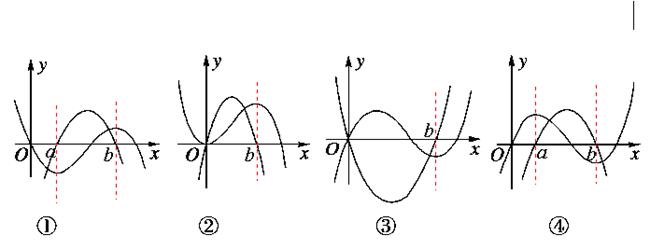
考点:函数的导数与函数单调性和关系.

练习册系列答案
相关题目
设函数 ,则
,则 ( )
( )
A.最大值为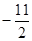 | B.最大值为 |
C.最小值为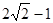 | D.最小值为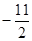 |
函数f(x)=x+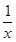 在x>0时有 ( ).
在x>0时有 ( ).
| A.极小值 | B.极大值 |
| C.既有极大值又有极小值 | D.极值不存在 |
设a∈R,若函数y=ex+ax,x∈R有大于零的极值点,则( )
| A.a<-1 | B.a>-1 |
C.a>- | D.a<- |
函数y=xlnx在区间(0,1)上是( )
| A.单调增函数 |
B.在(0, )上是减函数,在( )上是减函数,在( ,1)上是增函数 ,1)上是增函数 |
| C.单调减函数 |
D.在(0, )上是增函数,在( )上是增函数,在( ,1)上是减函数 ,1)上是减函数 |
若存在过点(1,0)的直线与曲线y=x3和y=ax2+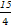 x-9都相切,则a等于( )
x-9都相切,则a等于( )
A.-1或-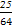 | B.-1或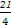 |
C.- 或- 或-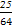 | D.- 或7 或7 |
已知函数f(x)及其导数f′(x),若存在x0,使得f(x0)=f′(x0),则称x0是f(x)的一个“巧值点”.下列函数中,有“巧值点”的是( )
①f(x)=x2;②f(x)=e-x;③f(x)=ln x;④f(x)=tan x;⑤f(x)=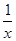 .
.
| A.①③⑤ | B.③④ | C.②③④ | D.②⑤ |
设函数f(x)满足x2f′(x)+2xf(x)=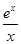 ,f(2)=
,f(2)=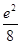 ,则x>0时,f(x)( ).
,则x>0时,f(x)( ).
| A.有极大值,无极小值 |
| B.有极小值,无极大值 |
| C.既有极大值又有极小值 |
| D.既无极大值也无极小值 |