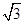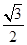题目内容
在△ABC中，内角A，B，C所对的边分别是a，b，c.已知bsin A＝3csin B，a＝3，cos B＝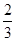
(1)求b的值；
(2)求sin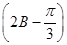
的值．
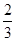
(1)求b的值；
(2)求sin
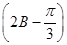的值．（1）
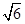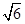（2）
（2）(1)在△ABC中，由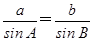
，
且bsin A＝3csin B，a＝3，
∴asin B＝3csin B，∴c＝1，
由b2＝a2＋c2－2accos B，cos B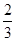＝，可得b＝.
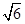(2)由cos B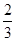＝，得sin B＝
，进而得
cos 2B＝2cos2B－1＝－
，sin 2B＝2sin Bcos B＝
.
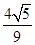所以sin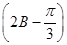＝sin 2Bcos
－cos 2Bsin＝
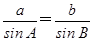，且bsin A＝3csin B，a＝3，
∴asin B＝3csin B，∴c＝1，
由b2＝a2＋c2－2accos B，cos B＝
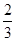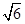，可得b＝.(2)由cos B＝
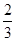，得sin B＝，进而得cos 2B＝2cos2B－1＝－
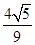，sin 2B＝2sin Bcos B＝.所以sin
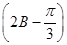＝sin 2Bcos－cos 2Bsin＝
练习册系列答案
黄冈360度定制密卷系列答案
阳光考场单元测试卷系列答案
名校联盟冲刺卷系列答案
名校提分一卷通系列答案
相关题目
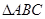中，角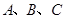
所对边分别为
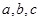，已知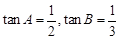
，且最长边的边长为
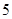.求：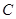
的正切值及其大小；
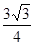，求a的值．
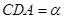，每批游客从各自报名点到C岛所需运输成本S元。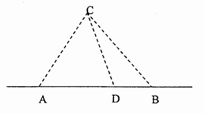
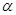的函数表达式，并指出
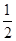c+bcosC.
,求b的最小值.
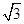，∠C＝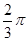
，则△ABC的面积为________．
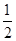b，且a＞b，则∠B＝( )．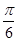
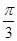
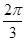
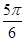
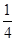，sin A＝
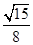，则a＝________，c＝________.
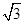，则S△ABC等于 ( )．
