题目内容
在△ABC中,内角A,B,C的对边分别为a,b,c.若asin Bcos C+csin Bcos A= b,且a>b,则∠B=( ).
b,且a>b,则∠B=( ).
 b,且a>b,则∠B=( ).
b,且a>b,则∠B=( ).A. | B. | C. | D. |
A
由条件得 sin Bcos C+
sin Bcos C+ sin Bcos A=
sin Bcos A= ,
,
由正弦定理,得sin Acos C+sin Ccos A= ,
,
∴sin(A+C)= ,从而sin B=
,从而sin B= ,
,
又a>b,且B∈(0,π),因此B= .
.
 sin Bcos C+
sin Bcos C+ sin Bcos A=
sin Bcos A= ,
,由正弦定理,得sin Acos C+sin Ccos A=
 ,
,∴sin(A+C)=
 ,从而sin B=
,从而sin B= ,
,又a>b,且B∈(0,π),因此B=
 .
.
练习册系列答案
相关题目
 ,且
,且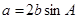 .
. 的大小;
的大小; ,求
,求 的面积及
的面积及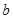 .
. 中,角
中,角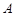 、
、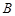 、
、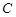 对的边分别为
对的边分别为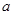 、
、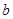 、
、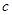 ,且
,且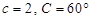
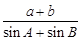 的值;
的值; ,求
,求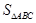 .
.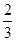
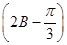 的值.
的值. bc,sin C=2
bc,sin C=2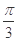 ,△ABC的面积S=
,△ABC的面积S= ,则sinC=( )
,则sinC=( )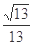
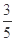

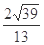
 中,
中, ,
, ,
, ,则
,则 .
.