题目内容
.(本题满分14分)已知函数f(x)=sin(ωx+φ),其中ω>0,|φ|<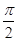 .
.
(1)若cos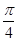 cosφ-sin
cosφ-sin sinφ=0,求φ的值;
sinφ=0,求φ的值;
(2)在(1)的条件下,若函数f(x)的图象的相邻两条对称轴之间的距离等于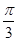 ,求函数f(x)的解析式;并求最小正实数m,使得函数f(x)的图象向左平移m个单位后所对应的函数是偶函数.
,求函数f(x)的解析式;并求最小正实数m,使得函数f(x)的图象向左平移m个单位后所对应的函数是偶函数.
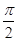 .
.(1)若cos
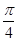 cosφ-sin
cosφ-sin sinφ=0,求φ的值;
sinφ=0,求φ的值;(2)在(1)的条件下,若函数f(x)的图象的相邻两条对称轴之间的距离等于
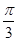 ,求函数f(x)的解析式;并求最小正实数m,使得函数f(x)的图象向左平移m个单位后所对应的函数是偶函数.
,求函数f(x)的解析式;并求最小正实数m,使得函数f(x)的图象向左平移m个单位后所对应的函数是偶函数.解: (1)由cos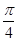 cosφ-sin
cosφ-sin sinφ=0得cos
sinφ=0得cos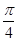 cosφ-sin
cosφ-sin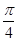 sinφ=0,
sinφ=0,
即cos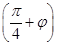 =0. ……….(3分)
=0. ……….(3分)
又|φ|<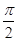 ,∴φ=
,∴φ=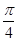 ;……….(6分)
;……….(6分)
(2)由(1)得,f(x)=sin .依题意,
.依题意,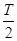 =
=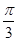 .
.
又T=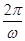 ,故ω=3,∴f(x)=sin
,故ω=3,∴f(x)=sin ………..(9分)
………..(9分)
函数f(x)的图象向左平移m个单位后,所得图象对应的函数为g(x)=sin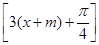 ,
,
g(x)是偶函数当且仅当3m+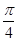 =kπ+
=kπ+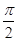 (k∈Z),
(k∈Z),
即m=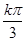 +
+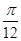 (k∈Z).
(k∈Z).
从而,最小正实数m=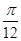 .……….(12分)
.……….(12分)
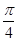 cosφ-sin
cosφ-sin sinφ=0得cos
sinφ=0得cos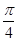 cosφ-sin
cosφ-sin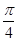 sinφ=0,
sinφ=0,即cos
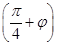 =0. ……….(3分)
=0. ……….(3分)又|φ|<
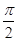 ,∴φ=
,∴φ=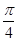 ;……….(6分)
;……….(6分)(2)由(1)得,f(x)=sin
 .依题意,
.依题意,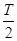 =
=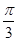 .
.又T=
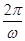 ,故ω=3,∴f(x)=sin
,故ω=3,∴f(x)=sin ………..(9分)
………..(9分)函数f(x)的图象向左平移m个单位后,所得图象对应的函数为g(x)=sin
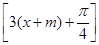 ,
,g(x)是偶函数当且仅当3m+
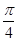 =kπ+
=kπ+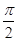 (k∈Z),
(k∈Z),即m=
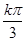 +
+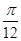 (k∈Z).
(k∈Z).从而,最小正实数m=
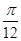 .……….(12分)
.……….(12分)略

练习册系列答案
 导学全程练创优训练系列答案
导学全程练创优训练系列答案
相关题目
 sin(3x—
sin(3x— ) 的定义域是__________,值域是________,周期是________,振幅是________,初相是_________.
) 的定义域是__________,值域是________,周期是________,振幅是________,初相是_________. 中,角
中,角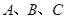 所对的边分别为
所对的边分别为 ,向量
,向量 ,且
,且 .
. 的值;
的值; 
 ,求
,求 .
.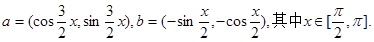
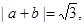 求x的值;
求x的值;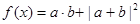 ,若
,若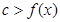 恒成立,求实数c的取值范围.
恒成立,求实数c的取值范围. 是函数
是函数 图象的一条对称轴,当
图象的一条对称轴,当 取最小正数时
取最小正数时 在
在 单调递增
单调递增 单调递减
单调递减 单调递减
单调递减 单调递增
单调递增 的图象上所有点的横坐标伸长到原来的
的图象上所有点的横坐标伸长到原来的 倍(纵坐标不变),再将所得图象向左平移
倍(纵坐标不变),再将所得图象向左平移 个单位,则所得函数图象对应的解析式为
个单位,则所得函数图象对应的解析式为



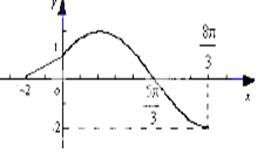
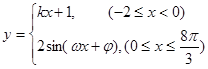 的图像如下图,则( )
的图像如下图,则( ) 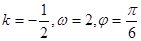
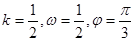
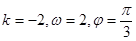
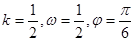
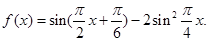
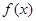 的最小正周期;
的最小正周期;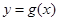 的图像与函数
的图像与函数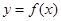 的图像关于原点对称,求
的图像关于原点对称,求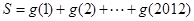 的值。
的值。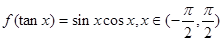 则
则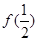 =
=