题目内容
函数f(x)=x|x+a|+b是奇函数的充要条件是( )
| A.ab="0" | B.a+b="0" | C.a=b | D.a2+b2=0 |
D
若a2+b2=0,即a=b=0,
此时f(-x)=(-x)|x+0|+0=-x·|x|=-(x|x+0|+b)=-(x|x+a|+b)=-f(x).
∴a2+b2=0是f(x)为奇函数的充分条件,又若f(x)=x|x+a|+b是奇函数,即f(-x)=(-x)|(-x)+a|+b=-f(x),则必有a=b=0,即a2+b2=0.
∴a2+b2=0是f(x)为奇函数的必要条件.
此时f(-x)=(-x)|x+0|+0=-x·|x|=-(x|x+0|+b)=-(x|x+a|+b)=-f(x).
∴a2+b2=0是f(x)为奇函数的充分条件,又若f(x)=x|x+a|+b是奇函数,即f(-x)=(-x)|(-x)+a|+b=-f(x),则必有a=b=0,即a2+b2=0.
∴a2+b2=0是f(x)为奇函数的必要条件.

练习册系列答案
相关题目
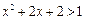 的解集为R,q:不等式
的解集为R,q:不等式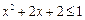 的解集为
的解集为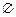
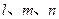 表示不同的直线,
表示不同的直线,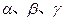 表示不同的平面,给出下列4个命题:
表示不同的平面,给出下列4个命题: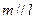 ,且
,且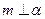 ,则
,则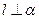 ;
;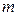 ∥
∥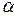 ,则
,则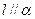 ;
;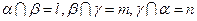 ,则
,则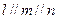 ;
;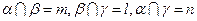 ,且
,且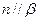 ,则
,则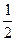 <x<
<x<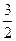 ,则实数a的取值范围是( )
,则实数a的取值范围是( )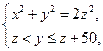 的正整数解组
的正整数解组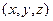 的个数.
的个数.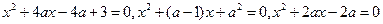 至少有一个方程有实数根,求实数
至少有一个方程有实数根,求实数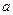 的取值范围。
的取值范围。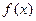 存在导函数,则
存在导函数,则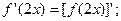
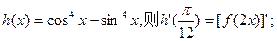
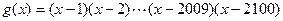 ,则
,则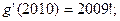
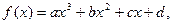 则
则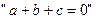 是“
是“