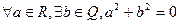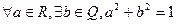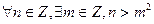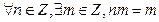题目内容
写出由下述各命题构成的“p或q”,“p且q”,“非p”形式的复合命题,并指出所构成的这些复合命题的真假。
(1)p:5是17的约数,q:5是15的约数.
(2)p:方程x2-1=0的解是x="1, " q:方程x2-1=0的解是x=-1,
(3)p:不等式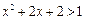 的解集为R,q:不等式
的解集为R,q:不等式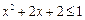 的解集为
的解集为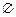
(1)p:5是17的约数,q:5是15的约数.
(2)p:方程x2-1=0的解是x="1, " q:方程x2-1=0的解是x=-1,
(3)p:不等式
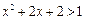 的解集为R,q:不等式
的解集为R,q:不等式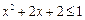 的解集为
的解集为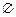
见解析
[解题思路]:写三种形式的复合命题时,在命题p或命题q的语句中,由于中文表达的习惯常常会有些省略,这种情况下应作词语上的调整。判断复合命题真假时,关键是判断简单命题的真假,再按真值表来判断即可.
(1)p或q:5是17或15的约数;
p且q:5是17与15的公约数,(或写成:9是17的约数,且9是15的约数);
非p:5不是17的约数.
∵p假,q真,∴“p或q”为真,“p且q” 为假,而“非p”为真.
(2)p或q:方程x2-1=0的解是x=1,或方程x2-1=0的解是x=-1
(注意,不能写成“方程x2-1=0的解是x=±1”,这与真值表不符);
p且q:方程x2-1=0的解是x=1,且方程x2-1=0的解是x=-1;
非p:方程x2-1=0的解不都是x=1(注意,在命题p中的“是”应理解为“都是”的意思);
∵p假,q假,∴“p或q”与“p且q” 均为假,而“非p”为真.
(3)p或q:不等式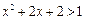 的解集为R或不等式
的解集为R或不等式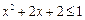 的解集为
的解集为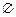 .
.
p且q:不等式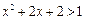 的解集为R或不等式
的解集为R或不等式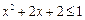 的解集为
的解集为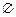
非p:不等式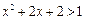 的解集为
的解集为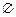 .
.
∵p真,q假,∴“p或q”为真,“p且q” 为假,而“非p”为假.
(1)p或q:5是17或15的约数;
p且q:5是17与15的公约数,(或写成:9是17的约数,且9是15的约数);
非p:5不是17的约数.
∵p假,q真,∴“p或q”为真,“p且q” 为假,而“非p”为真.
(2)p或q:方程x2-1=0的解是x=1,或方程x2-1=0的解是x=-1
(注意,不能写成“方程x2-1=0的解是x=±1”,这与真值表不符);
p且q:方程x2-1=0的解是x=1,且方程x2-1=0的解是x=-1;
非p:方程x2-1=0的解不都是x=1(注意,在命题p中的“是”应理解为“都是”的意思);
∵p假,q假,∴“p或q”与“p且q” 均为假,而“非p”为真.
(3)p或q:不等式
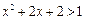 的解集为R或不等式
的解集为R或不等式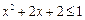 的解集为
的解集为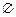 .
.p且q:不等式
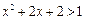 的解集为R或不等式
的解集为R或不等式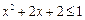 的解集为
的解集为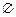
非p:不等式
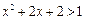 的解集为
的解集为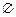 .
.∵p真,q假,∴“p或q”为真,“p且q” 为假,而“非p”为假.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 ”命题:
”命题: 的两个实数都为
的两个实数都为 是锐角三角形, 则
是锐角三角形, 则 ,则
,则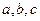 中至少有一个为
中至少有一个为 。
。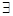 x∈Z,使x2+2x+m≤0”的否定是( )
x∈Z,使x2+2x+m≤0”的否定是( )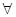 x∈Z使x2+2x+m≤0
x∈Z使x2+2x+m≤0 q”、“p
q”、“p q”、“
q”、“ p”形式的命题的真假.
p”形式的命题的真假. 是有理数,q:
是有理数,q: 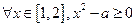 ”,命题q:“
”,命题q:“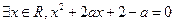 ”若命题“p且q”是真命题,则实数a的取值范围是___________.
”若命题“p且q”是真命题,则实数a的取值范围是___________.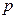 :对一切
:对一切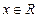 ,都有
,都有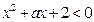 ,若
,若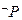 为真,求实数
为真,求实数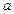 的取值范围。
的取值范围。