题目内容
如果不等式|x-a|＜1成立的充分不必要条件是
＜x＜
，则实数a的取值范围是( )
＜x＜，则实数a的取值范围是( )| A．＜a＜ | B．≤a≤ |
| C．a＞或a＜ | D．a≥或a≤ |
B
|x-a|＜1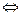
a-1＜x＜a+1,由题意可知{x|<x<}
{x|a-1<x<a+1}.
则有
解得≤a≤,
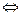a-1＜x＜a+1,由题意可知{x|<x<}{x|a-1<x<a+1}.则有
解得≤a≤,
练习册系列答案
阅读快车系列答案
相关题目
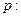方程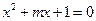
有两个不等的正实数根，命题
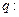方程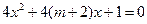
无实数根。若“
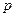或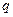
”为真命题，求
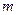的取值范围。
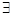x∈R，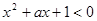
” 的否定是 
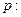“对于任意的实数
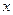都有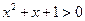
”的否定及符号表示，并判断是全称命题还是特称命题？
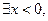有
”的否定是 .
.对此，四名同学做出了如下判断：
；
；
；
；
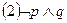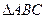中，若
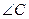是直角，则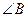
一定是锐角．”的证明过程如下：
，
，
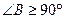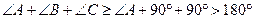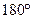矛盾，所以上述假设不成立，