题目内容
求满足下列关系式组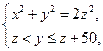 的正整数解组
的正整数解组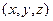 的个数.
的个数.
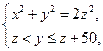 的正整数解组
的正整数解组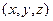 的个数.
的个数.131
[解] 令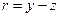 ,由条件知
,由条件知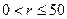 ,方程化为
,方程化为
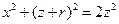 ,即
,即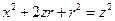 . (1)
. (1)
因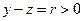 ,故
,故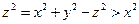 ,从而
,从而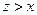 .
.
设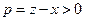 .因此(1)化为
.因此(1)化为
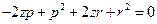 . (2)
. (2)
下分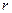 为奇偶讨论,
为奇偶讨论,
(ⅰ)当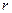 为奇数时,由(2)知
为奇数时,由(2)知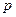 为奇数.
为奇数.
令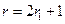 ,
,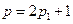 ,代入(2)得
,代入(2)得
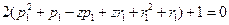 . (3)
. (3)
(3)式明显无整数解.故当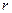 为奇数时,原方程无正整数解.
为奇数时,原方程无正整数解.
(ⅱ)当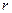 为偶数时,设
为偶数时,设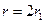 ,由方程(2)知
,由方程(2)知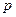 也为偶数.从而可设
也为偶数.从而可设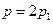 ,代入(2)化简得
,代入(2)化简得
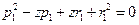 . (4)
. (4)
由(4)式有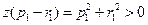 ,故
,故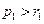 ,从而可设
,从而可设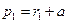 ,则(4)可化为
,则(4)可化为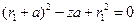 ,
,
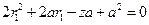 . (5)
. (5)
因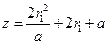 为整数,故
为整数,故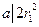 .
.
又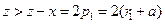 ,因此
,因此
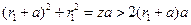 ,得
,得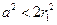 ,
,
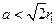 .
.
因此,对给定的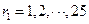 ,解的个数恰是满足条件
,解的个数恰是满足条件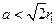 的
的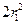 的正因数
的正因数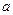 的个数
的个数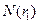 .因
.因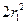 不是完全平方数,从而
不是完全平方数,从而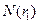 为
为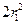 的正因数的个数
的正因数的个数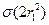 的一半.即
的一半.即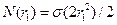 .
.
由题设条件,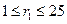 .而
.而
25以内有质数9个:2,3,5,7,11,13,17,19,23.将25以内的数分为以下八组::
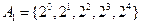 ,
,
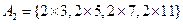 ,
,
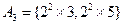 ,
,
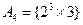 ,
,
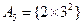 ,
,
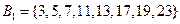 ,
,
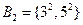 ,
,
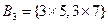 ,
,
从而易知
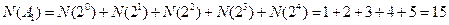
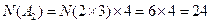 ,
,
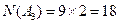 ,
,
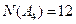 ,
,
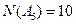 ,
,
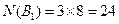 ,
,
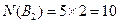 ,
,
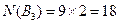 ,
,
将以上数相加,共131个.因此解的个数共131.
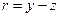 ,由条件知
,由条件知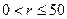 ,方程化为
,方程化为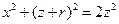 ,即
,即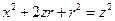 . (1)
. (1)因
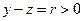 ,故
,故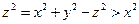 ,从而
,从而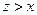 .
.设
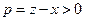 .因此(1)化为
.因此(1)化为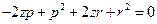 . (2)
. (2) 下分
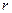 为奇偶讨论,
为奇偶讨论,(ⅰ)当
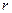 为奇数时,由(2)知
为奇数时,由(2)知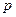 为奇数.
为奇数.令
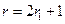 ,
,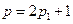 ,代入(2)得
,代入(2)得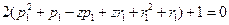 . (3)
. (3)(3)式明显无整数解.故当
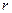 为奇数时,原方程无正整数解.
为奇数时,原方程无正整数解. (ⅱ)当
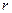 为偶数时,设
为偶数时,设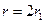 ,由方程(2)知
,由方程(2)知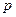 也为偶数.从而可设
也为偶数.从而可设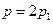 ,代入(2)化简得
,代入(2)化简得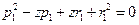 . (4)
. (4)由(4)式有
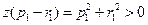 ,故
,故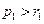 ,从而可设
,从而可设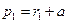 ,则(4)可化为
,则(4)可化为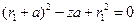 ,
,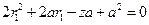 . (5)
. (5)因
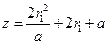 为整数,故
为整数,故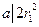 .
. 又
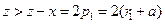 ,因此
,因此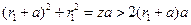 ,得
,得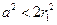 ,
,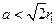 .
.因此,对给定的
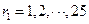 ,解的个数恰是满足条件
,解的个数恰是满足条件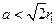 的
的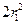 的正因数
的正因数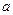 的个数
的个数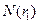 .因
.因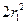 不是完全平方数,从而
不是完全平方数,从而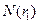 为
为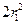 的正因数的个数
的正因数的个数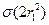 的一半.即
的一半.即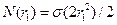 .
. 由题设条件,
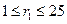 .而
.而25以内有质数9个:2,3,5,7,11,13,17,19,23.将25以内的数分为以下八组::
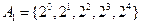 ,
,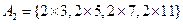 ,
,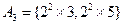 ,
,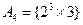 ,
,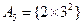 ,
,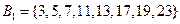 ,
,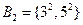 ,
,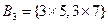 ,
,从而易知
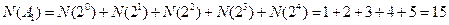
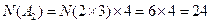 ,
,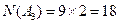 ,
,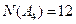 ,
,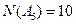 ,
,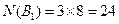 ,
,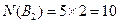 ,
,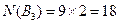 ,
,将以上数相加,共131个.因此解的个数共131.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 ,那么下列命题成立的是( )
,那么下列命题成立的是( ) 、
、 是第一象限角,则
是第一象限角,则 .
. .
.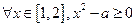 ”,命题q:“
”,命题q:“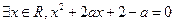 ”若命题“p且q”是真命题,则实数a的取值范围是___________.
”若命题“p且q”是真命题,则实数a的取值范围是___________.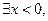 有
有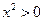 ”的否定是 .
”的否定是 .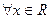 ,不等式
,不等式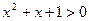 恒成立的否定是 ▲
恒成立的否定是 ▲ 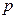 :对一切
:对一切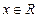 ,都有
,都有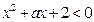 ,若
,若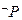 为真,求实数
为真,求实数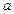 的取值范围。
的取值范围。