题目内容
一款击鼓小游戏的规则如下:每盘游戏都需要击鼓三次,每次击鼓要么出现一次音乐,要么不出现音乐;每盘游戏击鼓三次后,出现一次音乐获得10分,出现两次音乐获得20分,出现三次音乐获得100分,没有出现音乐则扣除200分(即获得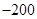 分).学科网设每次击鼓出现音乐的概率为
分).学科网设每次击鼓出现音乐的概率为 ,且各次击鼓出现音乐相互独立.
,且各次击鼓出现音乐相互独立.
(1)设每盘游戏获得的分数为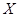 ,求
,求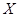 的分布列;
的分布列;
(2)玩三盘游戏,至少有一盘出现音乐的概率是多少?
(3)玩过这款游戏的许多人都发现,若干盘游戏后,与最初的分数相比,分数没有增加反而减少了.请运用概率统计的相关知识分析分数减少的原因.
(1)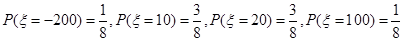 ;(2)
;(2)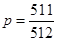 ;
;
(3)每盘所得分数的期望为负数,所以玩得越多,所得分数越少.
解析试题分析:(1)本题属于独立重复试验问题,利用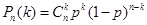 即可求得
即可求得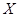 的分布列;(2)玩一盘游戏,没有出现音乐的概率为
的分布列;(2)玩一盘游戏,没有出现音乐的概率为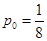 .“玩三盘游戏,至少有一盘出现音乐”的对立事件是“玩三盘游戏,三盘都没有出现音乐”由此可得“玩三盘游戏,至少有一盘出现音乐”的概率;(3)
.“玩三盘游戏,至少有一盘出现音乐”的对立事件是“玩三盘游戏,三盘都没有出现音乐”由此可得“玩三盘游戏,至少有一盘出现音乐”的概率;(3)
试题解答:(1)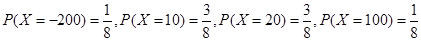 .所以
.所以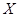 的分布列为
的分布列为
(2)玩一盘游戏,没有出现音乐的概率为X -200 10 20 100 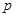
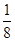
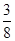
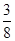
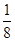
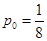 ,玩三盘游戏,至少有一盘出现音乐的概率为
,玩三盘游戏,至少有一盘出现音乐的概率为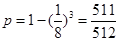 .
.
(3)由(1)得: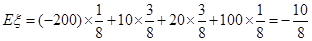 ,即每盘所得分数的期望为负数,所以玩得越多,所得分数越少的可能性更大.
,即每盘所得分数的期望为负数,所以玩得越多,所得分数越少的可能性更大.
【考点定位】1、随机变量的分布列;2、独立重复事件的概率;3、统计知识.

 阅读快车系列答案
阅读快车系列答案某超市为了解顾客的购物量及结算时间等信息,安排一名员工随机收集了在该超市购物的100位顾客的相关数据,如下表所示.
| 一次 购物量 | 1至 4件 | 5至 8件 | 9至 12件 | 13至 16件 | 17件及 以上 |
| 顾客数(人) | x | 30 | 25 | y | 10 |
| 结算时间 (分钟/人) | 1 | 1.5 | 2 | 2.5 | 3 |
已知这100位顾客中一次购物量超过8件的顾客占55%.
(1)确定x,y的值,并估计顾客一次购物的结算时间的平均值;
(2)求一位顾客一次购物的结算时间不超过2分钟的概率.(将频率视为概率)
某高校共有15000人,其中男生10500人,女生4500人,为调查该校学生每周平均体育运动时间的情况,采用分层抽样的方法,收集300位学生每周平均体育运动时间的样本数据(单位:小时)
(1)应收集多少位女生样本数据?
(2)根据这300个样本数据,得到学生每周平均体育运动时间的频率分布直方图(如图所示),其中样本数据分组区间为: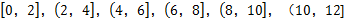 .估计该校学生每周平均体育运动时间超过4个小时的概率.
.估计该校学生每周平均体育运动时间超过4个小时的概率.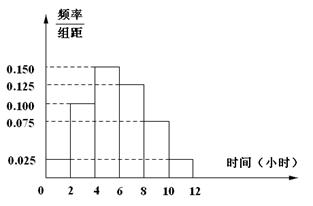
(3)在样本数据中,有60位女生的每周平均体育运动时间超过4个小时.请完成每周平均体育运动时间与性别的列联表,并判断是否有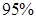 的把握认为“该校学生的每周平均体育运动时间与性别有关”.
的把握认为“该校学生的每周平均体育运动时间与性别有关”.
附: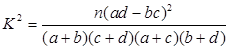
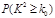 | 0.10 | 0.05 | 0.010 | 0.005 |
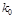 | 2.706 | 3.841 | 6.635 | 7.879 |
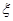 为取出的4个球中红球的个数,求
为取出的4个球中红球的个数,求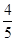 ,
,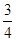 ,
,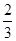 ,且每个问题回答正确与否相互独立.
,且每个问题回答正确与否相互独立. ,
, ,
, ,这三张卡片除标记的数字外完全相同。随机有放回地抽取
,这三张卡片除标记的数字外完全相同。随机有放回地抽取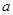 ,
,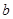 ,
,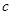 .
.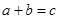 ”的概率;
”的概率;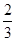 和
和 ,现安排甲组研发新产品
,现安排甲组研发新产品 ,乙组研发新产品
,乙组研发新产品 .设甲,乙两组的研发是相互独立的.
.设甲,乙两组的研发是相互独立的. 万元,若新产品
万元,若新产品 万元,求该企业可获得利润的分布列和数学期望.
万元,求该企业可获得利润的分布列和数学期望.