题目内容
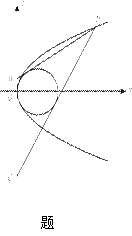
过抛物线y2=4x顶点O的直线l1、l2与抛物线的另一个交点分别为A、B,l1⊥l2,OD⊥AB,垂足为D,则D点的轨迹方程为( )
| A.y2=x(x≠0) | B.
| ||
| C.(x-2)2+y2=4(x≠0) | D.(x-2)2+y2=4 |
设直线OA的方程为y=kx,则
,消去y得x=
,
∴点A的坐标为(
,
),
∵l1⊥l2,
∴直线OA的方程为y=-
x,点B的坐标为(4k2,-4k),
则直线AB的斜率为
=
,
∴直线AB的方程为y+4k=
(x-4k2),
整理可得,y=
(x-4),
故直线AB经过定点(4,0),
∵OD⊥AB,垂足为D,则OD的垂直平分线必定经过点(2,0),
∴点(2,0)到原点O的距离等于到点D的距离,
又点(2,0)到原点O的距离为2,
∴点D到定点(2,0)的距离恒为定值2,
根据圆的定义可知,点D的轨迹是一个以(2,0)为圆心,2为半径的一个圆,
∴点D的轨迹方程为(x-2)2+y2=4,
故选:D.

|
| 4 |
| k2 |
∴点A的坐标为(
| 4 |
| k2 |
| 4 |
| k |
∵l1⊥l2,
∴直线OA的方程为y=-
| 1 |
| k |
则直线AB的斜率为
| ||
|
| k |
| 1-k2 |
∴直线AB的方程为y+4k=
| k |
| 1-k2 |
整理可得,y=
| k |
| 1-k2 |
故直线AB经过定点(4,0),
∵OD⊥AB,垂足为D,则OD的垂直平分线必定经过点(2,0),
∴点(2,0)到原点O的距离等于到点D的距离,
又点(2,0)到原点O的距离为2,
∴点D到定点(2,0)的距离恒为定值2,
根据圆的定义可知,点D的轨迹是一个以(2,0)为圆心,2为半径的一个圆,
∴点D的轨迹方程为(x-2)2+y2=4,
故选:D.


练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 是抛物线
是抛物线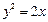 上的动点,点
上的动点,点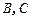 在
在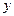 轴上,圆
轴上,圆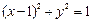 内切于
内切于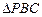 ,求
,求