题目内容
【题目】已知数列{an}的前n项和为Sn , 点(n, ![]() )在直线y=
)在直线y= ![]() x+
x+ ![]() 上.
上.
(1)求数列{an}的通项公式;
(2)设bn= ![]() ,求数列{bn}的前n项和为Tn , 并求使不等式Tn>
,求数列{bn}的前n项和为Tn , 并求使不等式Tn> ![]() 对一切n∈N*都成立的最大正整数k的值.
对一切n∈N*都成立的最大正整数k的值.
【答案】
(1)解:由题意,得 ![]() =
= ![]() ,化为Sn=
,化为Sn= ![]() .
.
故当n≥2时,an=Sn﹣Sn﹣1= ![]() ﹣
﹣ ![]() =n+5,
=n+5,
当n=1时,a1=S1=6=1+5,
∴an=n+5.
(2)解:bn= ![]() =
= ![]() =
= ![]() ,
,
∴Tn= ![]() +…+
+…+ ![]()
= ![]() =
= ![]() .
.
由于Tn+1﹣Tn= ![]() =
= ![]() >0,
>0,
因此Tn单调递增,
故(Tn)min=1.
令1 ![]() ,解得k<20,
,解得k<20,
∴kmax=19
【解析】(1)由题意,得 ![]() =
= ![]() ,化为Sn=
,化为Sn= ![]() . 利用递推关系即可得出.(2)利用“裂项求和”可得Tn , 再利用数列的单调性、不等式的性质即可得出.
. 利用递推关系即可得出.(2)利用“裂项求和”可得Tn , 再利用数列的单调性、不等式的性质即可得出.
【考点精析】通过灵活运用数列的前n项和和数列的通项公式,掌握数列{an}的前n项和sn与通项an的关系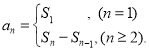 ;如果数列an的第n项与n之间的关系可以用一个公式表示,那么这个公式就叫这个数列的通项公式即可以解答此题.
;如果数列an的第n项与n之间的关系可以用一个公式表示,那么这个公式就叫这个数列的通项公式即可以解答此题.

练习册系列答案
相关题目
【题目】某学校为倡导全体学生为特困学生捐款,举行“一元钱,一片心,诚信用水”活动,学生在购水处每领取一瓶矿泉水,便自觉向捐款箱中至少投入一元钱.现统计了连续5天的售出和收益情况,如表:
售出水量x(单位:箱) | 7 | 6 | 6 | 5 | 6 |
收益y(单位:元) | 165 | 142 | 148 | 125 | 150 |
(1)求y关于x的线性回归方程;
(2)预测售出8箱水的收益是多少元?
附:回归直线的斜率和截距的最小二乘法估计公式分别为: ![]() =
= 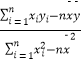 ,
, ![]() =
= ![]() ﹣
﹣ ![]()
![]() ,
,
参考数据:7×165+6×142+6×148+5×125+6×150=4420.