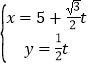Question

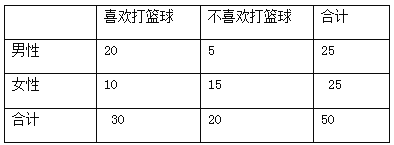
【题目】某高中为了解高中学生的性别和喜欢打篮球是否有关，对50名高中学生进行了问卷调查，得到如下列联表：

已知在这50人中随机抽取1人，抽到喜欢打篮球的学生的概率为

（Ⅰ）请将上述列联表补充完整；

（Ⅱ）判断是否有99.5%的把握认为喜欢打篮球与性别有关？

Answer 1

【答案】(1)见解析(2) 没有99.5%的把握认为喜欢打篮球与性别有关

【解析】分析：第一问利用条件在这50人中随机抽取1人，抽到喜欢打篮球的学生的概率为，求得喜欢打篮球的人数，从而求得不喜欢打篮球的人数，利用题中的表格可以补全结果，第二问根据列联表求得的值，对照临界值可知没有99.5%的把握认为喜欢打篮球与性别有关.

详解：（Ⅰ）根据题意，喜欢打篮球的人数为50×=30，

则不喜欢打篮球的人数为20，

填写2×2列联表如下：

（Ⅱ）根据列联表中数据，计算

K2===3＜7.879，

对照临界值知，没有99.5%的把握认为喜欢打篮球与性别有关．