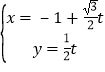Question

【题目】如图所示，在四棱锥S ABCD中，平面SAD⊥平面ABCD．四边形ABCD为正方形，

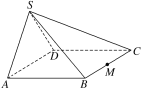
(1)求证：CD⊥平面SAD．

(2)若SA＝SD，点M为BC的中点，在棱SC上是否存在点N，使得平面DMN⊥平面ABCD？若存在，请说明其位置，并加以证明；若不存在，请说明理由．

Answer 1

【答案】（1）见解析；（2）见解析

【解析】

(1) 先证明CD⊥AD，再证明CD⊥平面SAD；（2）存在点N为SC的中点，连接PC，DM交于点O，连接DN，PM，SP，NM，ND，NO，先证明NO⊥平面ABCD，即证平面DMN⊥平面ABCD.

(1)证明：因为四边形ABCD为正方形，所以CD⊥AD．

又因为平面SAD⊥平面ABCD，且平面SAD∩平面ABCD＝AD，

所以CD⊥平面SAD．

(2)存在点N为SC的中点，使得平面DMN⊥平面ABCD．

证明如下：如图，连接PC，DM交于点O，连接DN，PM，SP，NM，ND，NO，

因为PD∥CM，且PD＝CM，

所以四边形PMCD为平行四边形，

所以PO＝CO．

又因为点N为SC的中点，所以NO∥SP．

易知SP⊥AD，

因为平面SAD⊥平面ABCD，平面SAD∩平面ABCD＝AD，并且SP⊥AD，

所以SP⊥平面ABCD，

所以NO⊥平面ABCD．又因为NO平面DMN，

所以平面DMN⊥平面ABCD．