题目内容
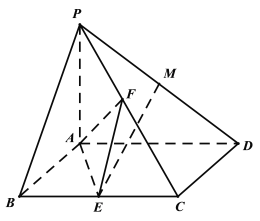
【题目】如图,直三棱柱![]() 中,
中,![]() ,
,![]() ,
,![]() 为
为![]() 的中点.
的中点.
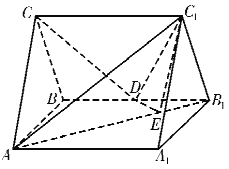
(I)若![]() 为
为![]() 上的一点,且
上的一点,且![]() 与直线
与直线![]() 垂直,求
垂直,求![]() 的值;
的值;
(Ⅱ)在(I)的条件下,设异面直线![]() 与
与![]() 所成的角为45°,求点
所成的角为45°,求点![]() 到平面
到平面![]() 的距离.
的距离.
【答案】(Ⅰ) ![]() (Ⅱ)
(Ⅱ) ![]()
【解析】
(Ⅰ) 取![]() 中点
中点![]() ,可知
,可知![]() ,利用面面垂直可证得
,利用面面垂直可证得![]() 平面
平面![]() ,进而得到
,进而得到![]() ,根据线面垂直性质得
,根据线面垂直性质得![]() ,从而可证得
,从而可证得![]() ;从而利用平行线分线段成比例求得结果;(Ⅱ)利用
;从而利用平行线分线段成比例求得结果;(Ⅱ)利用![]() ,根据异面直线成角和分别求解出所需线段长和
,根据异面直线成角和分别求解出所需线段长和![]() ,从而构造方程求解出点到面的距离.
,从而构造方程求解出点到面的距离.
(Ⅰ)证明:取![]() 中点
中点![]() ,连接
,连接![]()
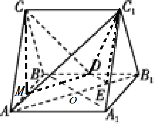
![]() 为
为![]() 中点,则有
中点,则有![]()
![]()
![]()
又因为三棱柱![]() 为直三棱柱
为直三棱柱 ![]() 平面
平面![]() 平面
平面![]()
![]() 平面
平面![]() 平面
平面![]()
![]() 平面
平面![]()
又![]() 平面
平面![]()
![]()
![]() ,
,![]() 平面
平面![]() ,
,![]() 平面
平面![]()
![]() 平面
平面![]() ,又
,又![]() 平面
平面![]()
![]()
![]()
![]()
连接![]() ,设
,设![]() ,因为
,因为![]() 为正方形
为正方形 ![]()
![]() 平面
平面![]() ,
,![]() 平面
平面![]()
![]()
![]() 为
为![]() 的中点
的中点 ![]() 为
为![]() 的中点
的中点 ![]()
(Ⅱ)由(Ⅰ)可知![]()
![]()
![]()
![]()
可求得![]()
由余弦定理可得:![]()
![]()
![]()
连接![]() ,连接
,连接![]()

在三棱锥![]() 及三棱锥
及三棱锥![]() 中,
中,
![]()
点![]() 到平面
到平面![]() 的距离为
的距离为![]()
又![]()
所以![]() ,即点
,即点![]() 到平面
到平面![]() 的距离为
的距离为![]()

练习册系列答案
相关题目
【题目】近年来,某地区积极践行“绿水青山就是金山银山”的绿色发展理念![]() 年年初至
年年初至![]() 年年初,该地区绿化面积
年年初,该地区绿化面积![]() (单位:平方公里)的数据如下表:
(单位:平方公里)的数据如下表:
年份 |
|
|
|
|
|
|
|
年份代号 |
|
|
|
|
|
|
|
绿化面积 |
|
|
|
|
|
|
|
(1)求![]() 关于
关于![]() 的线性回归方程;
的线性回归方程;
(2)利用(1)中的回归方程,预测该地区![]() 年年初的绿化面积,并计算
年年初的绿化面积,并计算![]() 年年初至
年年初至![]() 年年初,该地区绿化面积的年平均增长率约为多少.
年年初,该地区绿化面积的年平均增长率约为多少.
(附:回归直线的斜率与截距的最小二乘法估计公式分别为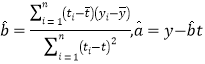 ,
,![]() )
)