题目内容
【题目】选修4-4:坐标系与参数方程
在平面直角坐标系![]() 中,直线
中,直线![]() 过原点且倾斜角为
过原点且倾斜角为![]() .以坐标原点
.以坐标原点![]() 为极点,
为极点,![]() 轴正半轴为极轴建立坐标系,曲线
轴正半轴为极轴建立坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .在平面直角坐标系
.在平面直角坐标系![]() 中,曲线
中,曲线![]() 与曲线
与曲线![]() 关于直线
关于直线![]() 对称.
对称.
(Ⅰ)求曲线![]() 的极坐标方程;
的极坐标方程;
(Ⅱ)若直线![]() 过原点且倾斜角为
过原点且倾斜角为![]() ,设直线
,设直线![]() 与曲线
与曲线![]() 相交于
相交于![]() ,
,![]() 两点,直线
两点,直线![]() 与曲线
与曲线![]() 相交于
相交于![]() ,
,![]() 两点,当
两点,当![]() 变化时,求
变化时,求![]() 面积的最大值.
面积的最大值.
【答案】(Ⅰ) ![]() (Ⅱ)
(Ⅱ) ![]()
【解析】
(Ⅰ)法一:将![]() 化为直角坐标方程,根据对称关系用
化为直角坐标方程,根据对称关系用![]() 上的点表示出
上的点表示出![]() 上点的坐标,代入
上点的坐标,代入![]() 方程得到
方程得到![]() 的直角坐标方程,再化为极坐标方程;法二:将
的直角坐标方程,再化为极坐标方程;法二:将![]() 化为极坐标方程,根据对称关系将
化为极坐标方程,根据对称关系将![]() 上的点用
上的点用![]() 上的点坐标表示出来,代入
上的点坐标表示出来,代入![]() 极坐标方程即可得到结果;(Ⅱ)利用
极坐标方程即可得到结果;(Ⅱ)利用![]() 和
和![]() 的极坐标方程与
的极坐标方程与![]() 的极坐标方程经
的极坐标方程经![]() 坐标用
坐标用![]() 表示,将所求面积表示为与
表示,将所求面积表示为与![]() 有关的三角函数解析式,通过三角函数值域求解方法求出所求最值.
有关的三角函数解析式,通过三角函数值域求解方法求出所求最值.
(Ⅰ)法一:由题可知,![]() 的直角坐标方程为:
的直角坐标方程为:![]() ,
,
设曲线![]() 上任意一点
上任意一点![]() 关于直线
关于直线![]() 对称点为
对称点为![]() ,
,
所以![]()
又因为![]() ,即
,即![]() ,
,
所以曲线![]() 的极坐标方程为:
的极坐标方程为:![]()
法二:由题可知,![]() 的极坐标方程为:
的极坐标方程为:![]()
![]() ,
,
设曲线![]() 上一点
上一点![]() 关于
关于![]()
![]() 的对称点为
的对称点为![]() ,
,
所以
又因为![]() ,即
,即![]() ,
,
所以曲线![]() 的极坐标方程为:
的极坐标方程为:![]()
(Ⅱ)直线![]() 的极坐标方程为:
的极坐标方程为:![]() ,直线
,直线![]() 的极坐标方程为:
的极坐标方程为:![]()
设![]() ,
,![]()
所以![]() 解得
解得![]() ,
,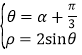 解得
解得![]()
![]()
![]()
因为:![]() ,所以
,所以![]()
当![]() 即
即![]() 时,
时,![]() ,
,![]() 取得最大值为:
取得最大值为:![]()

【题目】在抽取彩票“双色球”中奖号码时,有33个红色球,每个球的编号分别为01,02,…,33.一位彩民用随机数表法选取6个号码作为6个红色球的编号,选取方法是从下面的随机数表中第1行第6列的数字3开始,从左向右读数,则依次选出的第3个红色球的编号为( )
49 54 43 54 82 17 37 93 23 78 87 35 20 96 43 84 26 34 91 64 |
57 24 55 06 88 77 04 74 47 67 21 76 33 50 25 83 92 12 06 76 |
A.21B.32C.09D.20
【题目】为迎接2022年北京冬季奥运会,普及冬奥知识,某校开展了“冰雪答题王”冬奥知识竞赛活动.现从参加冬奥知识竞赛活动的学生中随机抽取了100名学生,将他们的比赛成绩(满分为100分)分为6组:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,得到如图所示的频率分布直方图.
,得到如图所示的频率分布直方图.
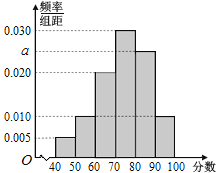
(1)求![]() 的值;
的值;
(2)估计这100名学生的平均成绩(同一组中的数据用该组区间的中点值为代表);
(3)在抽取的100名学生中,规定:比赛成绩不低于80分为“优秀”,比赛成绩低于80分为“非优秀”.请将下面的2×2列联表补充完整,并判断是否有99.9%的把握认为“比赛成绩是否优秀与性别有关”?
优秀 | 非优秀 | 合计 | |
男生 | 40 | ||
女生 | 50 | ||
合计 | 100 |
参考公式及数据:![]()
| 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
【题目】已知平面直角坐标系![]() ,直线
,直线![]() 过点
过点![]() ,且倾斜角为
,且倾斜角为![]() ,以
,以![]() 为极点,
为极点,![]() 轴的非负半轴为极轴建立极坐标系,圆
轴的非负半轴为极轴建立极坐标系,圆![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求直线![]() 的参数方程和圆
的参数方程和圆![]() 的标准方程;
的标准方程;
(2)设直线![]() 与圆
与圆![]() 交于
交于![]() 、
、![]() 两点,若
两点,若![]() ,求直线
,求直线![]() 的倾斜角的
的倾斜角的![]() 值.
值.
【题目】据统计,某地区植被覆盖面积![]() 公顷
公顷![]() 与当地气温下降的度数
与当地气温下降的度数![]() 之间呈线性相关关系,对应数据如下:
之间呈线性相关关系,对应数据如下:
| 20 | 40 | 60 | 80 |
| 3 | 4 | 4 | 5 |
![]() 请用最小二乘法求出y关于x的线性回归方程;
请用最小二乘法求出y关于x的线性回归方程;
![]() 根据
根据![]() 中所求线性回归方程,如果植被覆盖面积为300公顷,那么下降的气温大约是多少
中所求线性回归方程,如果植被覆盖面积为300公顷,那么下降的气温大约是多少![]() ?
?
参考公式:线性回归方程![]() ;其中
;其中![]() ,
,![]() .
.