题目内容
1.解不等式:(x2-2x+2)2-2(x2-2x+2)-3>0.分析 令t=x2-2x+2≥1,可得t2-2t-3>0,求得t>3,可得x2-2x-1>0,由此求得x的范围.
解答 解:令t=x2-2x+2=(x-1)2+1≥1,可得t2-2t-3>0,
求得t>3,或t<-1(舍去).
故有x2-2x+2>3,即x2-2x-1>0,求得x<1-$\sqrt{2}$或 x>1+$\sqrt{2}$,
故原不等式的解集为{x|x<1-$\sqrt{2}$或 x>1+$\sqrt{2}$}.
点评 本题主要考查一元二次不等式的解法,体现了整体代换的解题思想,属于基础题.

练习册系列答案
相关题目
12.如图,在矩形ABCD中,已知AB=2,BC=1,若在矩形ABCD中任取一点P,则点P满足|AP|≤1的概率为( )


| A. | $\frac{π}{8}$ | B. | $\frac{π}{16}$ | C. | $\frac{π}{32}$ | D. | $\frac{π}{64}$ |
3.在△ABC中,若A=60°,B=45°,a=3$\sqrt{2}$,则b=( )
| A. | 4$\sqrt{3}$ | B. | 2$\sqrt{3}$ | C. | $\sqrt{3}$ | D. | $\frac{\sqrt{3}}{2}$ |
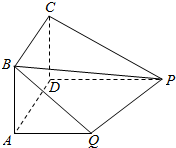 如图,四边形ABCD为正方形,PD⊥平面ABCD,PD∥QA,QA=AB=$\frac{1}{2}$PD=1.
如图,四边形ABCD为正方形,PD⊥平面ABCD,PD∥QA,QA=AB=$\frac{1}{2}$PD=1.