题目内容
一质点受到平面上的三个力F1,F2,F3(单位:牛顿)的作用而处于平衡状态.已知F1,F2成60°角,且F1,F2的大小分别为2和4,则F3的大小为( )
| A、6 | ||
| B、2 | ||
| C、8 | ||
D、2
|
考点:向量的加法及其几何意义
专题:平面向量及应用
分析:根据向量的合成法则以及向量的模长公式,进行计算即可.
解答:
解:根据题意,得;
|F3|=|F1+F2|
=
=
=2
,
∴F3的大小为2
.
故选:D.
|F3|=|F1+F2|
=
| F12+F22+2F1•F2 |
=
| 22+42+2×2×4×cos60° |
=2
| 7 |
∴F3的大小为2
| 7 |
故选:D.
点评:本题考查了平面向量的应用问题,解题时应平面向量的合成法则与向量的模长公式进行解答,是基础题.

练习册系列答案
相关题目
已知2
+
=(0,1),
=(1,-1),
•
=1,|
|=3,则
与
的夹角为 ( )
| a |
| b |
| c |
| a |
| c |
| b |
| b |
| c |
A、
| ||
B、
| ||
C、
| ||
D、
|
解下列不等式:
(1)|4x-3|<21;
(2)|
+2|≥
;
(3)
>
;
(4)|x+3|>x+3;
(5)|3x-4|>2x-1;
(6)|3x-4|≤x-1.
(1)|4x-3|<21;
(2)|
| x-1 |
| 2 |
| 3 |
| 4 |
(3)
| |3x-1|-1 |
| 2 |
| |1-3x|+1 |
| 3 |
(4)|x+3|>x+3;
(5)|3x-4|>2x-1;
(6)|3x-4|≤x-1.
已知数列{an}满足an+2=-an(n∈N*),且a1=1,a2=2,则该数列前2012项的和为( )
| A、-3 | B、3 | C、1 | D、0 |
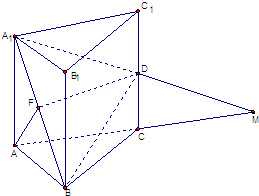 已知正三棱柱A1B1C1-ABC中,AA1=AB=a,D是CC1的中点,F是A1B的中点,A1D与AC的延长线交于点M(如图),
已知正三棱柱A1B1C1-ABC中,AA1=AB=a,D是CC1的中点,F是A1B的中点,A1D与AC的延长线交于点M(如图),