题目内容
如图，一个简单空间几何体的三视图其主视图与侧视图都是边长为2的正三角形，俯视图轮廓为正方形，则此几何体的侧面积是
A． | B．12 |
C． | D．8 |
D
解析试题分析：由三视图知：原几何体是一个正四棱锥，正四棱锥的底面边长为2，高为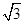
，所以侧面的斜高为
，所以该几何体的侧面积为
。
考点：三视图；四棱锥的侧面积。
点评：解决这类题的关键是准确分析出几何体的结构特征，发挥自己的空间想象力，把立体图形和平面图形进行对照，找出几何体中的数量关系。
练习册系列答案
相关题目
已知一个空间几何体的三视图如图所示，则这个几何体的表面积是
A． | B． | C． | D． |
一个球的表面积是
，那么这个球的体积为（ ）
A． | B． | C． | D． |
将边长
为的正方形ABCD沿对角线AC折起，使BD=，则三棱锥
的体积为（ ）
A． | B． | C． | D． |
已知球的直径SC=4，A，B是该球球面上的两点，AB=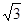
，
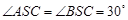，则棱锥S—ABC的体积为( )
A． | B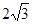． | C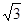． | D．1 |
一个多面体的三视图如图所示，其中正视图是正方形，侧视图是等腰三角形. 则该几何体的表面积为 （ ）
| A．16 | B．48 |
| C．60 | D．96 |
如图是一个空间几何体的三视图，则该几何体的侧面积为
A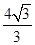． | B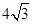． | C．8 | D．12 |